File:Penplot.jpg

Fig.19.4 from page 280 of book «Superfunctions»^[1], 2020.

This picture is used also as Рис.19.4 at page 266 of the Russian version «Суперфункции»^[2], 2014.

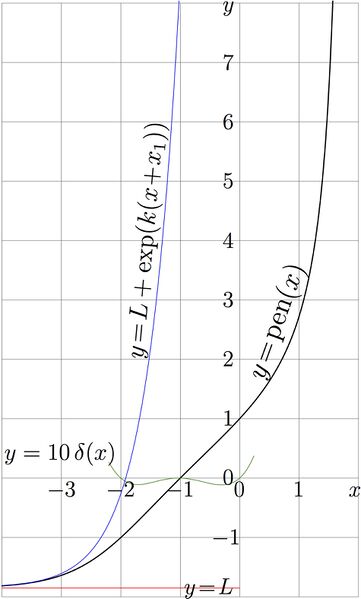
The picture represents the explicit plot of natural pentation.

\(y=\mathrm{pen}(x)\) is shown with thick black line.

The thin red line shows it asymptotic level \(L\approx -1.8503545290271812\) ; it is is smallest real fixed point of natural tetration.

The thin blue line shows the asymptotic

\( y=L+\exp(k(x+x_1)) \)

where \( k\approx 1.86573322821 \)

and \(x_1 \approx 2.24817451898 \)

The thin green line shown the deviation of the natural pentation from the linear approximation

\( \mathrm{linear}(x)=1+x \)

The deviation is defined as \(~ \delta=\delta(x)=\mathrm{pen}(x)-\mathrm{linear}(x) \)

In the range \(-2.1\!<\!x\!<\!1.1\), the deviation is small, the linear approximation provides 2 correct significant digits. In order to make the deviation visible, it is scaled with factor 10, so, \(y=10\delta(x)\) is plotted.

Description of natural pentation

Natiral pentation is specific superfunction of natural tetration (implementation fsexp.cin is available); the natural pentation safisfies the transfer equation

\(\mathrm{pen}(z\!+\!1) = \mathrm{tet}\Big( \mathrm{pen}(z)\Big)\)

The additional condition \( \mathrm{pen}(1)=\mathrm e \approx 2.71\) is assumed.

The regular behaviour at \( \pm \mathrm i \infty \) is assumed as an additional requirement; it is expected to provide the ubnigueness of the natural pentation.

Natural pentation is specific superfunction, it is constructed with regular iteration at the lowest real fixed point of natural tetration, denoted with \(L\).

The construction and evaluation of natural tetration is described also at Mathematics of Computation ^[3], 2009.

The construction and evaluation of natural pentation is described also at Applied and Computational Mathematics ^[4], 2014.

C++ generator of curves

\* Files ado.cin, fsexp.cin, fslog.cin should be loaded in order to compile the C++ code below*/

 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
#include <complex>
typedef std::complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
 #include "ado.cin"
 #include "fsexp.cin"
 #include "fslog.cin"

z_type pen0(z_type z){ 
DB Lp=-1.8503545290271812; 
DB k,a,b;
//      k=1.86573322821; a=-.62632418; b=0.4827;
        k=1.86573322821; a=-.6263241; b=0.4827;

z_type e=exp(k*z);
return Lp + e*(1.+e*(a+b*e));
}

z_type pen7(z_type z){ DB x; int m,n; z=pen0(z+(2.24817451898-7.));
DO(n,7) { if(Re(z)>8.) return 999.;  z=FSEXP(z);  if(abs(z)<40) goto L1; return 999.; L1: ;}
return z; }

z_type pen(z_type z){ DB x; int m,n;
x=Re(z); if(x<= -4.) return pen0(z); 
m=int(x+5.);
z-=DB(m); 
z=pen0(z);
DO(n,m) z=FSEXP(z);
return z;
}

int  main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
FILE *o;o=fopen("penplo.eps","w");  ado(o,608,1008);
 fprintf(o,"404 204 translate\n 100 100 scale\n");
#define M(x,y) fprintf(o,"%8.4f %8.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%8.4f %8.4f L\n",0.+x,0.+y);
 for(m=-4;m<3;m++) {M(m,-2)L(m,8)}
 for(n=-2;n<11;n++) {M(  -4,n)L(2,n)} fprintf(o,"2 setlinecap 1 setlinejoin .004 W 0 0 0 RGB S\n");

DO(n,150){x=-4+.04*n;y=Re(pen7(x)); if(n==0) M(x,y)else L(x,y); if(y>8.)break;} fprintf(o,".02 W 0 0 0 RGB S\n");

DO(n,150){x=-2.2+.04*n;y=10.*(Re(pen7(x))-(1.+x)); if(n==0) M(x,y)else L(x,y); if(y>.3)break;} fprintf(o,".01 W 0 .5 0 RGB S\n");

DB L=-1.8503545290271812;
DB K=1.86573322821;
DB a=-.6263241; 
DB b=0.4827;
DO(n,80){x=-4.+.04*n; DB e=exp(K*(x+2.24817451898));    y=L+e; 
        if(n==0) M(x,y) else L(x,y); if(y>8.) break;}
fprintf(o,".01 W 0 0 1 RGB S\n");

/*
DO(n,60){x=-4+.04*n; DB e=exp(K*(x+2.24817451898));     y=L+e*(1.+e*(a)); 
        if(n==0) M(x,y) else L(x,y); if(y>8.||y<-2.) break;}
*/
M(-4,L)L(0,L)
fprintf(o,".01 W 1 0 0 RGB S\n");


/*
DO(n,60){x=-4+.04*n; DB e=exp(K*(x+2.24817451898));     y=L+e*(1.+e*(a+e*b)); 
        if(n==0) M(x,y) else L(x,y); if(y<-2.) break;}
fprintf(o,".01 W 1 0 0 RGB S\n");
*/

DB t2=M_PI/1.86573322821;
DB tx=-2.32;
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);

printf("pen7(-1)=%18.14f\n", Re(pen7(-1.)));
printf("Pi/1.86573322821=%18.14f  %18.14f\n", M_PI/1.86573322821, 2*M_PI/1.86573322821);

        system("epstopdf penplo.eps"); 
        system(    "open penplo.pdf");
}

Latex generator of labels

\documentclass[12pt]{article}
\paperwidth 608px
\paperheight 1008px
\textwidth 1394px
\textheight 1300px
\topmargin -104px
\oddsidemargin -90px
\usepackage{graphics}
\usepackage{rotating}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\newcommand \rmi {\mathrm{i}}
\begin{document}
{\begin{picture}(608,1008)
%\put(12,0){\ing{24}}
%\put(12,0){\ing{penma}}
\put(0,0){\ing{penplo}}
\put(377,994){\sx{3.2}{$y$}}
\put(377,895){\sx{3.2}{$7$}}
\put(377,795){\sx{3.2}{$6$}}
\put(377,695){\sx{3.2}{$5$}}
\put(377,594){\sx{3.2}{$4$}}
\put(377,494){\sx{3.2}{$3$}}
\put(377,394){\sx{3.2}{$2$}}
\put(377,294){\sx{3.2}{$1$}}
\put(377,194){\sx{3.2}{$0$}}
\put(358, 93){\sx{3.2}{$-1$}}
\put(80,174){\sx{3.2}{$-3$}}
\put(180,174){\sx{3.2}{$-2$}}
\put(280,174){\sx{3.2}{$-1$}}
\put(396,174){\sx{3.2}{$0$}}
\put(496,174){\sx{3.2}{$1$}}
\put(590,174){\sx{3.2}{$x$}}
\put(242,406){\sx{3.6}{\rot{85}$y\!=\!L+\exp(k(x\!+\!x_1))$\ero}}
%
%\put(560,510){\sx{3.6}{\rot{84}$y\!=\!L+\exp(k(x\!+\!x_1))$\ero}}
%\put(532,708){\sx{3.6}{\rot{86}$y\!=\!\mathrm{pen}(x)$\ero}}
\put(446,370){\sx{3.9}{\rot{70}$y\!=\!\mathrm{pen}(x)$\ero}}
%\put(366,236){\sx{2.3}{$y\!=\!10(\mathrm{pen}(x)\!-\!1\!-\!x)$}}
%\put(416,239){\sx{3.4}{$y=10\,\delta(x)$}}
\put(8,236){\sx{3.3}{$y=10\,\delta(x)$}}
%\put(366,  8){\sx{3.3}{$L$}}
\put(312,  9){\sx{3.2}{$y\!=\!L$}}
\end{picture}
\end{document}

References

Keywords

«Ackermann», «Explicit plot», «Exponential», «Natural pentation», «Natural tetration», «Pentation», «Superfunction», «Superfunctions», «Tetration», «AMS»,

«Суперфункции»,