Sandbox
From: Fig.17.2, p.239 in Superfunctions.
Tetration is the superfunction of the exponential map. For a given base \(b\), tetration is the function \(\operatorname{tet}_b\) satisfying the functional equation \[ \operatorname{tet}_b(z+1)=b^{\operatorname{tet}_b(z)}\,, \] together with additional normalization conditions that ensure uniqueness. The name “tetration’’ reflects its position as the next operation after exponentiation in the hyperoperation hierarchy.
The most commonly studied case is the real holomorphic tetration to base \(b=\mathrm e\), usually denoted simply by \[ \operatorname{tet}(z)=\operatorname{tet}_{\mathrm e}(z). \]
Definition
Let \(T_b(z)=b^z\). A function \(F\) is called a superexponential (superfunction of \(T_b\)) if \[ F(z+1)=T_b(F(z)). \] A tetration to base \(b\) is the unique real holomorphic superexponential satisfying the regularity condition \[ \lim_{y\to\pm\infty} F(x+\mathrm i y) = \text{finite} \] and the normalization \[ F(0)=1. \]
These conditions distinguish tetration from the infinitely many other superfunctions of the same transfer equation.
Properties
For the principal tetration \(\operatorname{tet}_b\), the following hold:
- **Shift property** (transfer equation)
\[ \operatorname{tet}_b(z+1)=b^{\operatorname{tet}_b(z)}. \]
- **Derivative at the fixed point**
If \(L\) is the fixed point of the exponential, satisfying \(L=b^L\), then \[ \operatorname{tet}'_b(0)=L. \]
- **Analyticity**
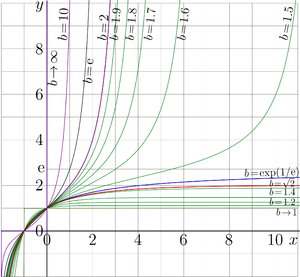
For \(1< b < \mathrm e^{1/\mathrm e}\), the tetration to base \(b\) extends to an entire function. For larger bases, branch singularities appear.
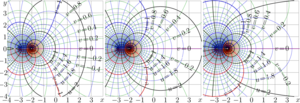
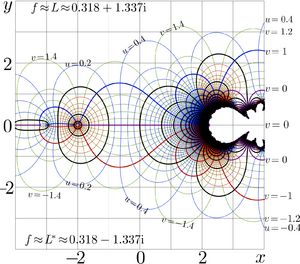
Complex structure
From: Fig.19.7, p.266 in Superfunctions.
The complex dynamics of \(z\mapsto b^z\) determine the analytic structure of tetration. For \(1<b<\mathrm e^{1/\mathrm e}\), the exponential has two attracting fixed points. This allows construction of a regular Abel function and hence an entire superfunction. At the critical base \(b=\mathrm e^{1/\mathrm e}\), these fixed points collide (bifurcation), and above this threshold, the dynamics become repelling, producing complex branches.
Relation to superfunctions
Tetration is the canonical superfunction of the exponential. Any superfunction \(F\) of \(T_b(z)=b^z\) satisfies the transfer equation \[ F(z+1)=b^{F(z)}. \] Among these, the tetration is the uniquely normalized superfunction that is:
- real on the real axis,
- holomorphic in a vertical strip,
- smooth at \(\pm\mathrm i\infty\),
- normalized by \(F(0)=1\).
Other superexponentials differ by periodic or quasiperiodic distortions.
Inverse: Abel function
The inverse of tetration is the Abel function (ArcTetration), denoted by \(\operatorname{ate}_b\). It satisfies the Abel functional equation \[ \operatorname{ate}_b(b^z)=\operatorname{ate}_b(z)+1, \] with normalization \(\operatorname{ate}_b(1)=0\). For the natural exponential, this becomes \[ \operatorname{ate}(\exp(z))=\operatorname{ate}(z)+1. \]
Iterates
The pair \((\operatorname{tet}_b, \operatorname{ate}_b)\) provides analytic interpolation of integer iterates. For the \(n\)-th iterate of the exponential (not exponentiation), \[ \exp_b^n(z)=\operatorname{tet}_b\!\bigl(n+\operatorname{ate}_b(z)\bigr), \] where \(n\) may be any real or complex number.
This gives a smooth functional continuation of exponentiation to non-integer “heights’’.
Special cases
From: Fig.17.4, p.245 in Superfunctions.
Base \(b=\mathrm e^{1/\mathrm e}\)
This base is the threshold at which the exponential map changes from having two attracting fixed points to having none. The tetration at this base has unusual properties, such as:
- extremely slow growth near its fixed point,
- increased sensitivity to initial conditions,
- non-entire analytic structure.
Base \(b=\mathrm e\)
The standard tetration \(\operatorname{tet}(z)\) is real and smooth on the entire real line. Its values decrease towards the lower fixed point of the exponential as \(z\to-\infty\), and blow up super-exponentially as \(z\to+\infty\).
Historical remarks
The modern construction of real analytic tetration was developed by:
- E. Schröder and G. Koenigs (19th century) — regular iteration theory
- J. Kneser (1949) — analytic solution for base \(b=\mathrm e\)
- D. Kouznetsov and H. Trappmann (2009–2024) — complex extension, superfunctions, explicit computation methods
A unified presentation is given in the monograph Superfunctions.
Examples and plots
From: Fig.14.4, p.203 in Superfunctions.
Some characteristic graphs:
- Real tetration \(\operatorname{tet}(x)\)
- Complex level sets of tetration
- Abel function \(\operatorname{ate}(x)\)
- Iterates \(\exp^n(x)\) for fractional \(n\)
From: Fig.18.3 (top), p.250 in Superfunctions.
Humor
Source: free illustration.
References
D. Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020. Includes all figures cited above.
Keywords
«Superfunction», «Exponential», «Logarithm», «Tetration», «ate», «Abel function», «Transfer equation», «Iterates».