File:QuadraticMapByChatGPTtest11.jpg
Revision as of 09:11, 30 August 2025 by T (talk | contribs) ({{oq|QuadraticMapByChatGPTtest11.jpg|QuadraticMapByChatGPTtest11.jpg (351 × 351 pixels, file size: 100 KB, MIME type: image/jpeg)}} Complex map of function \(z \mapsto z^2 \) in the complex z-plane generated as a test of routine conto01.cin written by ChatGPT 2025.08.29. ==Generator== <pre> #include <stdio.h> #include <stdlib.h> #define DB double #define DO(x,y) for(x=0;x<y;x++) #include<complex> typedef std::complex<double> z_type; #define Re(x) x.real() #define Im(x) x.imag() #d...)
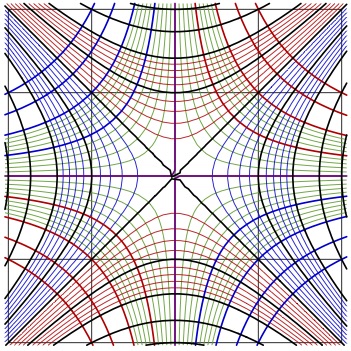
QuadraticMapByChatGPTtest11.jpg (351 × 351 pixels, file size: 100 KB, MIME type: image/jpeg)
Summary
Complex map of function \(z \mapsto z^2 \) in the complex z-plane
generated as a test of routine conto01.cin written by ChatGPT 2025.08.29.
Generator
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include<complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto01.cin"
z_type F(z_type z) {return z*z;}
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
int M=41,M1=M+1;
int N=41,N1=N+1;
DB X[M1],Y[N1]; DB *g, *f, *w; // w is working array.
g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
char v[M1*N1]; // v is working array
FILE *o;o=fopen("QuadraticMapByChatGPTtest11.eps","w"); ado(o,422,422);
fprintf(o,"210 210 translate\n 100 100 scale\n");
fprintf(o,"1 setlinejoin 2 setlinecap\n");
fprintf(o,"/W { setlinewidth } def\n");
fprintf(o,"/RGB { setrgbcolor } def\n");
fprintf(o,"/S { stroke } def\n");
#define M(x,y) fprintf(o,"%6.3f %6.3f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.3f %6.3f L\n",0.+x,0.+y);
DO(m,M1) X[m]=-2+.1*(m-.4);
DO(n,N1) Y[n]=-2+.1*(n-.3);
for(m=-2;m<3;m++){M(m,-2) L(m,2)}
for(n=-2;n<3;n++){M(-2,n) L(2,n)}
fprintf(o,".01 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){ g[m*N1+n]=999;
f[m*N1+n]=999;}
DO(m,M1){x=X[m]; if(m/10*10==m) printf("x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); //if(abs(z+2.)>.019)
c=F(z);
p=Re(c); q=Im(c); if(p>-99 && p<99 ){ g[m*N1+n]=p;f[m*N1+n]=q;}
}}
fprintf(o,"1 setlinejoin 1 setlinecap\n"); p=3.;q=2.;
fprintf(o,".01 W 0 .6 0 RGB S\n"); for(m=-2;m<2;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);
fprintf(o,".01 W .8 0 0 RGB S\n"); for(m=0;m<2;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);
fprintf(o,".01 W 0 0 .8 RGB S\n"); for(m=0;m<2;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);
fprintf(o,".02 W 0 0 .8 RGB S\n"); for(m= 1;m<5;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);
fprintf(o,".02 W .8 0 0 RGB S\n"); for(m= 1;m<5;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);
fprintf(o,".02 W .5 0 .5 RGB S\n"); conto(o,f,w,v,X,Y,M,N, (0. ),-2*p,2*p);
fprintf(o,".02 W 0 0 0 RGB S\n"); for(m=-10;m<11;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);
fprintf(o,"showpage\n"); fprintf(o,"%c%cTrailer\n",'%','%');
fclose(o); free(f); free(g); free(w);
system("epstopdf QuadraticMapByChatGPTtest11.eps");
system( "open QuadraticMapByChatGPTtest11.pdf"); //for macintosh
}
conto01.cin
// conto01.cin
// Safe, small marching-squares contour tracer (drop-in replacement for conto.cin)
// API (keeps compatibility with older mains):
// void ado(FILE* o, double width, double height);
// void MM(double x, double y); // draw small tick/mark at (x,y)
// void LL(double x, double y); // draw small tick/mark or label helper
// double conto(FILE* o, double *field, double *work, char *vis,
// double *X, double *Y, int M, int N, double level, double vmin, double vmax);
//
// Notes:
// - field is expected as field[m*(N+1) + n], where m in [0..M], n in [0..N] (grid points M+1 by N+1).
// - M,N are cell counts (so there are M+1 and N+1 grid points).
// - This implementation writes multiple short stroked segments. It is robust (bounds-checked).
//
// Usage: include into your main and call ado(o, w,h) to start PostScript, then call conto(...) repeatedly.
#include <cstdio>
#include <cmath>
#include <vector>
#include <string>
#include <cstring>
#ifndef DB
#define DB double
#endif
// PostScript header writer
static FILE* _ps_out = nullptr;
static DB _ps_w = 0, _ps_h = 0;
static bool _ps_started = false;
void ado(FILE* o, double width, double height){
_ps_out = o;
_ps_w = width; _ps_h = height;
_ps_started = true;
if(!o) return;
fprintf(o,"%%!PS-Adobe-3.0 EPSF-3.0\n");
fprintf(o,"%%%%BoundingBox: 0 0 %d %d\n", (int)width, (int)height);
fprintf(o,"/M { moveto } def\n");
fprintf(o,"/L { lineto } def\n");
fprintf(o,"/S { stroke } def\n");
// small default style
fprintf(o,"1 setlinejoin 1 setlinecap\n");
fflush(o);
}
// Small tick helper: draws a tiny line centered at (x,y) in user coords
void MM(double x, double y){
if(!_ps_out) return;
double dx = 0.05, dy = 0.05;
fprintf(_ps_out,"newpath %g %g moveto %g %g lineto stroke\n", x-dx, y, x+dx, y);
}
void LL(double x, double y){
if(!_ps_out) return;
double dx = 0.05, dy = 0.05;
fprintf(_ps_out,"newpath %g %g moveto %g %g lineto stroke\n", x, y-dy, x, y+dy);
}
// Internal helper: write a stroked segment between two points
static inline void _ps_seg(FILE* o, double x1, double y1, double x2, double y2){
if(!o) return;
fprintf(o,"newpath %g %g moveto %g %g lineto stroke\n", x1, y1, x2, y2);
}
// Linear interpolation helper
static inline double interp(double a, double b, double va, double vb, double level){
if (fabs(vb - va) < 1e-18) return (a + b) * 0.5; // degenerate: return midpoint
return a + (b-a) * ( (level - va) / (vb - va) );
}
// Marching squares lookup: each case yields 0,1, or 2 segments. We'll handle ambiguous cases with center test.
static const int edge_pairs[16][4] = {
{-1,-1,-1,-1},//0
{0,3,-1,-1}, //1
{0,1,-1,-1}, //2
{1,3,-1,-1}, //3
{1,2,-1,-1}, //4
{0,1,2,3}, //5 ambiguous (saddle) -> will be resolved by center test
{0,2,-1,-1}, //6
{2,3,-1,-1}, //7
{2,3,-1,-1}, //8 (mirror)
{0,2,-1,-1}, //9
{0,3,1,2}, //10 ambiguous
{1,2,-1,-1}, //11
{1,3,-1,-1}, //12
{0,1,-1,-1}, //13
{0,3,-1,-1}, //14
{-1,-1,-1,-1} //15
};
// Map edge index -> endpoints (in local cell coordinates [0..1])
// edge 0: between (0,0)-(1,0) bottom
// edge 1: between (1,0)-(1,1) right
// edge 2: between (1,1)-(0,1) top
// edge 3: between (0,1)-(0,0) left
static inline void edge_point(int edge, int i, int j, double* X, double* Y, double* field, int M, int N, double level, double &rx, double &ry){
// X and Y are grid point arrays of length M+1 and N+1 respectively
// i in [0..M-1], j in [0..N-1] identifies cell
int N1 = N + 1;
double v00 = field[i*N1 + j];
double v10 = field[(i+1)*N1 + j];
double v11 = field[(i+1)*N1 + (j+1)];
double v01 = field[i*N1 + (j+1)];
if(edge==0){
double x = interp(X[i], X[i+1], v00, v10, level);
double y = Y[j];
rx = x; ry = y; return;
} else if(edge==1){
double x = X[i+1];
double y = interp(Y[j], Y[j+1], v10, v11, level);
rx = x; ry = y; return;
} else if(edge==2){
double x = interp(X[i+1], X[i], v11, v01, level);
double y = Y[j+1];
rx = x; ry = y; return;
} else { // edge==3
double x = X[i];
double y = interp(Y[j+1], Y[j], v01, v00, level);
rx = x; ry = y; return;
}
}
// Determine center value (for ambiguous cases)
static inline double cell_center_value(int i, int j, double* field, int M, int N){
int N1 = N + 1;
double v00 = field[i*N1 + j];
double v10 = field[(i+1)*N1 + j];
double v11 = field[(i+1)*N1 + (j+1)];
double v01 = field[i*N1 + (j+1)];
return 0.25*(v00+v10+v11+v01);
}
// Main contour function
DB conto(FILE* o, double *field, double *work, char *vis, double *X, double *Y,
int M, int N, double level, double vmin, double vmax)
{
// Inputs:
// field: array length (M+1)*(N+1) indexed as field[m*(N+1) + n]
if (!o) return 0.0;
if (!field || !X || !Y) return 0.0;
int M1 = M + 1, N1 = N + 1;
// safety checks
if (M <= 0 || N <= 0) return 0.0;
// For each cell, evaluate case and emit segment(s)
for(int i=0;i<M;i++){
for(int j=0;j<N;j++){
// read corner values
double v00 = field[i*N1 + j];
double v10 = field[(i+1)*N1 + j];
double v11 = field[(i+1)*N1 + (j+1)];
double v01 = field[i*N1 + (j+1)];
int b0 = (v00 > level) ? 1 : 0;
int b1 = (v10 > level) ? 1 : 0;
int b2 = (v11 > level) ? 1 : 0;
int b3 = (v01 > level) ? 1 : 0;
int idx = b0 | (b1<<1) | (b2<<2) | (b3<<3);
// no intersection or full cell: skip
if (idx == 0 || idx == 15) continue;
// handle ambiguous saddle cases (5 and 10) by center test
int pairs[4] = {-1,-1,-1,-1};
if (idx==5 || idx==10){
double center = cell_center_value(i,j,field,M,N);
if ( (idx==5 && center > level) || (idx==10 && center <= level) ){
// connect as two diagonals (0-1 and 2-3) -> edges [0,1] and [2,3] or [0,3] etc.
if(idx==5){
pairs[0]=0; pairs[1]=1; pairs[2]=2; pairs[3]=3;
} else {
pairs[0]=0; pairs[1]=3; pairs[2]=1; pairs[3]=2;
}
} else {
// alternate diagonal
if(idx==5){
pairs[0]=0; pairs[1]=3; pairs[2]=1; pairs[3]=2;
} else {
pairs[0]=0; pairs[1]=1; pairs[2]=2; pairs[3]=3;
}
}
} else {
// use lookup table
for(int k=0;k<4;k++) pairs[k] = edge_pairs[idx][k];
}
// emit segments for each valid pair
for(int k=0;k<4;k+=2){
int eA = pairs[k];
int eB = pairs[k+1];
if (eA < 0 || eB < 0) break;
double ax, ay, bx, by;
edge_point(eA, i, j, X, Y, field, M, N, level, ax, ay);
edge_point(eB, i, j, X, Y, field, M, N, level, bx, by);
// safety: coords finite?
if (!std::isfinite(ax) || !std::isfinite(ay) || !std::isfinite(bx) || !std::isfinite(by)) continue;
// emit small segment
_ps_seg(o, ax, ay, bx, by);
}
}
}
return 1.0;
}
References
Keywords
«ChatGPT», «Conto.cin», «Conto01.cin», «ContoTestQuadraticMap»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 09:11, 30 August 2025 |  | 351 × 351 (100 KB) | T (talk | contribs) | {{oq|QuadraticMapByChatGPTtest11.jpg|QuadraticMapByChatGPTtest11.jpg (351 × 351 pixels, file size: 100 KB, MIME type: image/jpeg)}} Complex map of function \(z \mapsto z^2 \) in the complex z-plane generated as a test of routine conto01.cin written by ChatGPT 2025.08.29. ==Generator== <pre> #include <stdio.h> #include <stdlib.h> #define DB double #define DO(x,y) for(x=0;x<y;x++) #include<complex> typedef std::complex<double> z_type; #define Re(x) x.real() #define Im(x) x.imag() #d... |
You cannot overwrite this file.
File usage
The following 2 pages use this file: