File list
Jump to navigation
Jump to search
This special page shows all uploaded files.
| Date | Name | Thumbnail | Size | User | Description | Versions |
|---|---|---|---|---|---|---|
| 10:13, 29 January 2026 | AteSuFacMapV.png (file) |  |
125 KB | T | {{oq|AteSuFacMapV.png|Original file (1,319 × 1,295 pixels, file size: 125 KB, MIME type: image/png)|480}} Complex map of combination of natural ArcTetration and SuperFactorial: \(f(z)=\mathrm{ate}\Big(\mathrm{SuFac}(z)\Big)\) The map is shown in the top picture with lines \(u=\Re \big(\mathrm{f}(x\!+\!\mathrm i y)\big)\) and lines \(v=\Im \big(\mathrm{f}(x\!+\!\mathrm i y)\big)\) in the \(x,y\) plane. The view of the map hints the conjecture about the asymptotic of... | 1 |
| 21:32, 28 January 2026 | AteSuExq2plotU.png (file) | 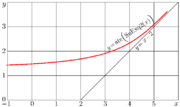 |
11 KB | T | == Summary == {{oq|AteSuExq2plotU.png|AteSuExq2plotU.png (737 × 438 pixels, file size: 11 KB, MIME type: image/png)}} Explicit plot of combination of natural ArcTetration and growing SuperExponential to base \(\sqrt{2}\): \(y=\mathrm{ate}\Big(\mathrm{SuExq2}(x)\Big)\) Here \(\mathrm{SuExq2}\) is SuperExponential to base \(\sqrt{2}\) constricted as regular iteration at fixed point 4 and placed so that \(\ \mathrm{SuExq2}(0)\!=\!1\ \). == C++ == /* ado.cin, <!--[[Con... | 1 |
| 21:31, 28 January 2026 | AteSuExq2mapU.png (file) |  |
183 KB | T | {{oq|AteSuExq2mapU.png|Original file (2,511 × 1,706 pixels, file size: 183 KB, MIME type: image/png)|400|}} Complex map of combination of two functions: natural ArcTetration «ate» and growing superexponential to base \(\sqrt{2}\). \(f(z)=\mathrm{ate}\Big(\mathrm{SuExq2}(z)\Big)\) The map is shown with lines \(u=\Re \big(f(x\!+\!\mathrm i y)\big)\) and lines \(v=\Im \big(f(x\!+\!\mathrm i y)\big)\) in the \(x,y\) plane. ==C++ generator of curves== /* files ado.cin, [[Co... | 1 |
| 15:29, 28 January 2026 | FactoriAsymp9ageeT.png (file) | 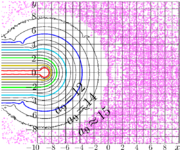 |
68 KB | T | {{oq|FactoriAsymp9ageeT.png|Original file (800 × 667 pixels, file size: 68 KB, MIME type: image/png)|400}} Map of agreement \(a_9\) for displaced Stirling asymptotic for Factorial: \[ A(z)= \sqrt{2\pi z}\ \exp\left(\log\left(\frac{z}{\mathrm e} \right) z + \frac{1}{12 z}\left(1+ \frac{1}{z^2}\left(\frac{-1}{30}+ \frac{1}{z^2}\left(\frac{1}{105}+ \frac{1}{z^2}\left(\frac{-1}{140}+ \frac{1}{z^2}\left(\frac{1}{99}+ \frac{1}{z^2}\left(\frac{-691}{30030} \right) \right) \right) \right)... | 1 |
| 20:38, 21 January 2026 | GammaAsymptoBgreeT.png (file) | 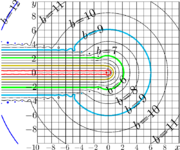 |
26 KB | T | {{oq|GammaAsymptoBgreeT.png|Original file (800 × 667 pixels, file size: 26 KB, MIME type: image/png)|400}} Agreement of Gamma function (implemented through the Factorial from fac.cin) with its asymptotic by <ref name="DLMF"> https://dlmf.nist.gov/5.11 About the Project 5 Gamma Function .. The expansion (5.11.1) is called Stirling’s series (Whittaker and Watson (1927, §12.33)), whereas the expansion (5.11.3), or sometimes just its leading term, is known as Stirling’s formula... | 1 |
| 18:03, 20 January 2026 | FactoriAsymptoBgreeT.png (file) |  |
25 KB | T | {{oq|FactoriAsymptoBgreeT.png|Original file (800 × 667 pixels, file size: 24 KB, MIME type: image/png) |400}} Map of agreement \[ b(z) = - \lg \left(\frac {|z!-B(z)|} {|z!|+|B(z)|} \right) \] of the asymptotic \( B(z)= \sqrt{2\pi z}\ \exp\left(\log\left(\frac{z}{\mathrm e} \right) z \right) \left(1+ \frac{1}{z}\left(\frac{1}{12}+ \frac{1}{z}\left(\frac{1}{288}+ \frac{1}{z}\left(\frac{-139}{51840}+ \frac{1}{z}\left(\frac{-571}{2488320}+ \frac{1}{z}\left(\frac{163879}{209018880}+ \frac... | 1 |
| 19:48, 19 January 2026 | FactoriAsymptoAgreeT.png (file) |  |
51 KB | T | misprint in the code had been corrected | 2 |
| 10:02, 17 January 2026 | Z2sin1zMapT.png (file) | 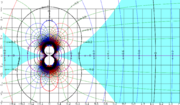 |
118 KB | T | {{oq|Z2sin1zMapT.png|Original file (1,933 × 1,124 pixels, file size: 118 KB, MIME type: image/png)|400}} Complex map of function \(f= z \mapsto z^2\sin(1/z) \ \). Notation: \( u+\mathrm i v = f(x\!+\!\mathrm i y)\ \); levels \(u=\mathrm{const}\) and levels \(v=\mathrm{const}\) are drawn. The conditional asymptotic \( z \mapsto 0\ \) takes place at \( z \to 0 \ , |\Im(z)|<\Re(z)^2\) : \[ \lim_{z\to 0,\ |\Im(z)|<\Re(z)^2 } f(z)=0 \] Range \(|y|<x^2\) in the map is shaded. The [[unco... | 1 |
| 16:55, 12 January 2026 | AuTraMapT.jpg (file) |  |
569 KB | T | smaller size, better view | 2 |
| 22:39, 11 January 2026 | Autraplot.jpg (file) |  |
127 KB | T | corrected misprint in the label | 2 |