Difference between revisions of "File:Anka616map.jpg"

Latest revision as of 16:01, 20 August 2025

Anka616map.jpg is complex map of Anka function

\[ \mathrm{Anka}(z)= \exp(\mathrm{ArcTania}(z))=\exp(z+\ln(z)-1)= \frac{1}{\mathrm e} \, z \exp(z)=\frac{1}{\mathrm e} \, \mathrm{zex}(z) \]

where zex is elementary functions, \(\mathrm{zex}(z)=z\ \exp(z)\)

Anka appears as the Schroeder function for the transfer function Doya, and satisfies the Schroeder equation

\[ \mathrm{Anka}(\mathrm{Doya}(z)) = \mathrm e \, \mathrm{Anka}(z) \]

Superfunctions

Anka616map.jpg appears as Fig.6.5 at page 69 of book Superfunctions ^[1]^[2]
in order to show better the sense of the Schroederfunctions as analogies of Abelfunctions and Scalefunctions as analogies of Superfunctions.

C++ generator of map

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//using namespace std;
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
z_type ArcTania(z_type z) {return z + log(z) - 1. ;}
z_type ArcTaniap(z_type z) {return 1. + 1./z ;}
z_type TaniaTay(z_type z) { int n; z_type s;
s=1.+z*(.5+z*(1./16.+z*(-1./192.+z*(-1./3072.+z*(1.3/6144.+z*(-4.7/147456.
//+z*(7.3/4128768.) //some reserve term
)))))); DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }
z_type TaniaNega(z_type z){int n;z_type s=exp(z-exp(z)+1.); 
DO(n,4) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }
z_type TaniaBig(z_type z){int n;z_type s=z; s=z-log(s)+1.; 
DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }
z_type TaniaS(z_type z){int n; z_type s,t=z+z_type(2.,-M_PI);t*=2./9.; t=I*sqrt(t);
s=-1.+t*(3.+t*(-3.+t*(.75+t*(.3+t*(.9/16.+t*(-.3/7.+t*(-12.51/224. //+t*(-.9/28.)
)))))));
DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }
z_type Tania(z_type z){ z_type t;
if( fabs(Im(z))< M_PI && Re(z)<-2.51) return TaniaNega(z);
if( abs(z)>7. || Re(z)>3.8 ) return TaniaBig(z);
if( Im(z) > .7 ) return TaniaS(z);
if( Im(z) < -.7) return conj(TaniaS(conj(z)));
return TaniaTay(z);
}

int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
 int M=520,M1=M+1;
 int N=601,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
// FILE *o;o=fopen("taniacontour.eps","w");ado(o,1620,1620);
//FILE *o;o=fopen("23.eps","w");ado(o,1220,1220);
FILE *o;o=fopen("anka616ma.eps","w");ado(o,1220,1220);
fprintf(o,"610 610 translate\n 100 100 scale\n");
DO(m,M1) X[m]=-6.+.02*(m-.5);
DO(n,N1)Y[n]=-6.+.02*(n-.5);
for(m=-6;m<7;m++){if(m==0){M(m,-6.2)L(m,6.2)} else{M(m,-6)L(m,6)}}
for(n=-6;n<7;n++){     M(  -6,n)L(6,n)}
fprintf(o,".008 W 0 0 0 RGB 2 setlinecap S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); // z*=.1;        
        c=exp(ArcTania(z));
//      c=Tania(log(z)); 
        p=Re(c);q=Im(c);  
 if(p>-91. && p<91. &&  q>-91. && q<91. ){ g[m*N1+n]=p;f[m*N1+n]=q;}
        }}
fprintf(o,"1 setlinejoin 2 setlinecap\n");  p=3;q=.5;
for(m=-10;m<10;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q, q); fprintf(o,".008 W 0 .6 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q); fprintf(o,".008 W .9 0 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q); fprintf(o,".008 W 0 0 .9 RGB S\n");
for(m=1;m<17;m++)  conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".03 W .9 0 0 RGB S\n");
for(m=1;m<17;m++)  conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".03 W 0 0 .9 RGB S\n");
                   conto(o,f,w,v,X,Y,M,N, (0.  ),-p,p); fprintf(o,".03 W .6 0 .6 RGB S\n");
for(m=-16;m<17;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
/*
y= M_PI; for(m=0;m<60;m+=4) {x=-7.95+.1*m; M(x,y) L(x+.05,y)}
y=-M_PI; for(m=0;m<60;m+=4) {x=-7.95+.1*m; M(x,y) L(x+.05,y)}
fprintf(o,".07 W 1 .5 0 RGB S\n");
y= M_PI; for(m=2;m<60;m+=4) {x=-7.95+.1*m; M(x,y) L(x+.05,y)}
y=-M_PI; for(m=2;m<60;m+=4) {x=-7.95+.1*m; M(x,y) L(x+.05,y)}
fprintf(o,".07 W 0 .5 1 RGB S\n");
*/
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
       system("epstopdf anka616ma.eps");    
       system(    "open anka616ma.pdf");
       getchar(); system("killall Preview");
}

Latex generator of labels

\documentclass[12pt]{article} 
\paperwidth 1268px 
\paperheight 1260px 
\textwidth 1794px 
\textheight 1700px 
\topmargin -98px 
\oddsidemargin -70px 
\usepackage{graphics} 
\usepackage{rotating} 
\newcommand \sx {\scalebox} 
\newcommand \rot {\begin{rotate}} 
\newcommand \ero {\end{rotate}} 
\newcommand \ing {\includegraphics} 
\newcommand \rmi {\mathrm{i}} 
\begin{document}  
\parindent 0pt 
\sx{1}{\begin{picture}(1252,1230) 
%\put(40,20){\ing{suzexD1map}} 
%\put(40,20){\ing{ZexD6map}} 
%\put(50,20){\ing{olgama}} 
\put(50,20){\ing{anka616ma}} 
\put(18,1210){\sx{5}{$y$}}
\put(22,1116){\sx{4.5}{$5$}}
\put(22,1016){\sx{4.5}{$4$}}
\put(22,916){\sx{4.5}{$3$}}
\put(22,816){\sx{4.5}{$2$}}
\put(22, 716){\sx{4.5}{$1$}}
\put(22, 616){\sx{4.5}{$0$}}
\put(-16, 516){\sx{4.5}{$-1$}}
\put(-16, 416){\sx{4.5}{$-2$}}
\put(-16, 316){\sx{4.5}{$-3$}}
\put(-16, 216){\sx{4.5}{$-4$}}
\put(-16, 116){\sx{4.5}{$-5$}}
\put(-16,  16){\sx{4.5}{$-6$}}
\put(18, -20){\sx{4.5}{$-6$}}
\put(118, -20){\sx{4.5}{$-5$}}
\put(218, -20){\sx{4.5}{$-4$}}
\put(318, -20){\sx{4.5}{$-3$}}
\put(418, -20){\sx{4.5}{$-2$}}
\put(518, -20){\sx{4.5}{$-1$}}
\put(650, -20){\sx{4.5}{$0$}}
\put(750, -20){\sx{4.5}{$1$}}
\put(850, -20){\sx{4.5}{$2$}}
\put(950, -20){\sx{4.5}{$3$}}
\put(1050, -20){\sx{4.5}{$4$}}
\put(1150, -20){\sx{4.5}{$5$}}
\put(1234, -20){\sx{5}{$x$}}
%\put(952, 1454){\sx{6}{\rot{75}$v\!=\!1$\ero}} 
%\put(914, 216){\sx{6}{\rot{-77}$v\!=\!-1$\ero}} 
\put(186,1180){\sx{5}{\rot{4}$u\!=\!0$\ero}} 
\put(184,1002){\sx{5}{\rot{5}$v\!=\!0$\ero}} 
\put(182,816){\sx{5}{\rot{3}$u\!=\!0$\ero}} 
\put(180, 616){\sx{5}{$v\!=\!0$}}  % \put(1200, 614){\sx{6}{$v\!=\!0$}}
\put(180, 422){\sx{5}{\rot{-6}$u\!=\!0$\ero}} 
\put(180, 232){\sx{5}{\rot{-6}$v\!=\!0$\ero}} 
\put(180, 56){\sx{5}{\rot{-6}$u\!=\!0$\ero}} 
%
\put(564, 640){\sx{5}{\rot{59}$v\!=\!0$\ero}}
\put(652, 630){\sx{5}{\rot{38}$u\!=\!0$\ero}}
\put(752, 610){\sx{5}{\rot{52}$u\!=\!1$\ero}}
%
%
\put(1066, 899){\sx{5}{\rot{2}$v\!=\!16$\ero}}
\put(1066, 858){\sx{5}{\rot{3}$u\!=\!-16$\ero}}
%
\put(1066, 776){\sx{5}{\rot{1}$u\!=\!-16$\ero}}
\put(1066, 726){\sx{5}{\rot{2}$u\!=\!16$\ero}}
%
\put(1066, 648){\sx{5}{\rot{-1}$v\!=\!16$\ero}}%
\put(1066, 590){\sx{5}{\rot{1}$v\!=\!-16$\ero}}%
%
\put(1066, 518){\sx{5}{\rot{-1}$u\!=\!16$\ero}}
\put(1066, 470){\sx{5}{\rot{0}$u\!=\!-16$\ero}}
%
\put(1060, 390){\sx{5}{\rot{-3}$v\!=\!-16$\ero}}
\put(1060, 338){\sx{5}{\rot{-1}$v\!=\!16$\ero}}
%
\put(1040, 256){\sx{5}{\rot{-4}$u\!=\!-16$\ero}}
\put(1040, 200){\sx{5}{\rot{-2}$u\!=\!16$\ero}}
%
\put(1030, 106){\sx{5}{\rot{-5}$v\!=\!16$\ero}}
\put(1030, 60){\sx{5}{\rot{-3}$v\!=\!-16$\ero}}

\end{picture}} 
\end{document}

References

↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - 2020/7/28
↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.

Keywords

«Abelfunction», «Ernst Schroeder», «Regular iteration», «Scalefunction», «Schroederfunction», «Superfunctions»,

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	06:10, 1 December 2018		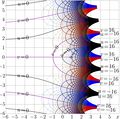2,641 × 2,625 (1.48 MB)	Maintenance script (talk \| contribs)	Importing image file

You cannot overwrite this file.

File usage

There are no pages that use this file.

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Horizontal resolution	150 dpi
Vertical resolution	150 dpi

[1] ttps://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - 2020/7/28

[2] ttps://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.

[1]

[2]

@@ Line 1: / Line 1: @@
+{{oq|Anka616map.jpg|}}
 '''Anka616map.jpg''' is [[complex map]] of [[Anka function]]
+\[
-$\mathrm{Anka}(z)= \exp(\mathrm{ArcTania}(z))=\exp(z+\ln(z)-1)= \frac{1}{\mathrm e} \, z \exp(z)=\frac{1}{\mathrm e} \, \mathrm{zex}(z)$
+\mathrm{Anka}(z)= \exp(\mathrm{ArcTania}(z))=\exp(z+\ln(z)-1)= \frac{1}{\mathrm e} \, z \exp(z)=\frac{1}{\mathrm e} \, \mathrm{zex}(z)
+\]
-where [[zex]] is elementary functions, $\mathrm{zex}(z)=z\,\exp(z)$
+where [[zex]] is elementary functions, \(\mathrm{zex}(z)=z\ \exp(z)\)
 Anka appears as the [[Schroeder function]] for the transfer function [[Doya function|Doya]], and satisfies the [[Schroeder equation]]
+\[
-$\mathrm{Anka}(\mathrm{Doya}(z)) = \mathrm e \, \mathrm{Anka}(z)$
+\mathrm{Anka}(\mathrm{Doya}(z)) = \mathrm e \, \mathrm{Anka}(z)
+\]
+==[[Superfunctions]]==
-==Usage==
-'''Anka616map.jpg''' is prepared to be used as figure 16.3  in book [[Superfunctions]]
+'''Anka616map.jpg''' appears as Fig.6.5 at page 69 of book [[Superfunctions]]
 <ref>
+https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - 2020/7/28
-http://mizugadro.mydns.jp/BOOK/437.pdf
+</ref><ref>
-D.Kouznetsov. Superfunctions (2015)
+https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). [[Superfunctions]]: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.
-</ref>.
+</ref><br>
+in order to show better the sense of the [[Schroederfunction]]s as analogies of
-==References==
+[[Abelfunction]]s and
+[[Scalefunction]]s as analogies of
+[[Superfunction]]s.
-<references/>
 ==[[C++]] generator of map==
+<pre>
-<poem><nomathjax><nowiki>
 #include <math.h>
 #include <stdio.h>
@@ Line 101: / Line 109: @@
        getchar(); system("killall Preview");
 }
+</pre>
-</nowiki></nomathjax></poem>
 ==[[Latex]] generator of labels==
+<pre>
-<poem><nomathjax><nowiki>
 \documentclass[12pt]{article}
 \paperwidth 1268px
@@ Line 191: / Line 199: @@
 \end{picture}}
 \end{document}
+</pre>
-</nowiki></nomathjax></poem>
+==References==
+{{ref}}
+{{fer}}
+==Keywords==
+«[[Abelfunction]]»,
+«[[Ernst Schroeder]]»,
+«[[Regular iteration]]»,
+«[[Scalefunction]]»,
+«[[Schroederfunction]]»,
+«[[Superfunctions]]»,
 [[Category:Book]]