Difference between revisions of "Abelpower"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
(file -> pic) |
||
| Line 1: | Line 1: | ||
| + | {{top}} |
||
| ⚫ | |||
| + | <div class="thumb tright" style="float:right; margin:-72px 0px 2px 12px; background-color:#fff"> |
||
| ⚫ | |||
| + | </div> |
||
| + | <div class="thumb tright" style="float:right; margin:2px 0px 2px 8px; background-color:#fff"> |
||
| ⚫ | |||
| − | + | {{pic|Adpow2map.jpg|300px}}<small><center>\(u\!+\!\mathrm i v\!=\!\mathrm{AdPow}_2(x\!+\!\mathrm i y)\)</center></small> |
|
| + | </div> |
||
| ⚫ | |||
[[Abelpower]] appears [[inverse function]] of the [[superpower]] function. |
[[Abelpower]] appears [[inverse function]] of the [[superpower]] function. |
||
| − | [[Abelpower]] is [[Abel function]] for the [[power function]], id est, transfer function \(T(z)\!=\!z^a\) |
+ | [[Abelpower]] is [[Abel function]] for the [[power function]], id est, that of the transfer function \(T(z)\!=\!z^a\) |
where \(a\) is parameter. Usually, it is assumed, that \(a\!>\!1\). |
where \(a\) is parameter. Usually, it is assumed, that \(a\!>\!1\). |
||
| + | |||
| + | This article presents a little bit extended spoiler of chapter 4.3 of book «[[Superfunctions]]» |
||
| + | <ref> |
||
| + | https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 |
||
| + | Dmitrii Kouznetsov. [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28 |
||
| + | </ref><ref> |
||
| + | https://mizugadro.mydns.jp/BOOK/468.pdf |
||
| + | Dmitrii Kouznetsov (2020). [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other [[superfunction]]s. Formulas, algorithms, tables, graphics. Publisher: [[Lambert Academic Publishing]]. |
||
| + | </ref> (pages 43-45); some relevant picture are added. |
||
| + | |||
==[[Superpower]] and [[Abelpower]]== |
==[[Superpower]] and [[Abelpower]]== |
||
| Line 43: | Line 58: | ||
\(u\!+\!\mathrm i v=G(x\!+\!\mathrm i y)\) |
\(u\!+\!\mathrm i v=G(x\!+\!\mathrm i y)\) |
||
| + | <div class="thumb tright" style="float:right; margin-2px 0px 2px 8px"> |
||
| − | |||
| − | + | {{pic|Apow2ma4.jpg|480px}}<small><center>zooming: \( ~ u\!+\!\mathrm i v=\mathrm{AuPow}_2(x\!+\!\mathrm i y)~ ~\) ; \(~ ~ u\!+\!\mathrm i v=\mathrm{AdPow}_2(x\!+\!\mathrm i y ) ~ ~ ~ \) |
|
| + | </center></small> |
||
| − | \(u\!+\!\mathrm i v=\mathrm{AdPow}_2(x\!+\!\mathrm i y)\)]] |
||
| + | </div> |
||
In the most of the complex plane, values of functions |
In the most of the complex plane, values of functions |
||
[[AuPow]]\(_a\) and |
[[AuPow]]\(_a\) and |
||
| Line 52: | Line 68: | ||
In order to compare the systems of cuts for these two functions, the zooming of the central parts of maps |
In order to compare the systems of cuts for these two functions, the zooming of the central parts of maps |
||
for [[AuPow]]\(_2\) and |
for [[AuPow]]\(_2\) and |
||
| − | [[AdPow]]\(_2\) are shown together in figure |
+ | [[AdPow]]\(_2\) are shown together in the last figure. |
==Application== |
==Application== |
||
| Line 65: | Line 81: | ||
==References== |
==References== |
||
| + | {{ref}} |
||
| − | <references/> |
||
| + | |||
| + | {{fer}} |
||
==Keywords== |
==Keywords== |
||
| − | [[Abel function]], |
+ | «[[Abel function]]», |
| − | [[ |
+ | «[[Abelfunction]]», |
| − | [[ |
+ | «[[Abelpower]]», |
| − | [[ |
+ | «[[AdPow]]», |
| − | [[ |
+ | «[[AuPow]]», |
| − | [[ |
+ | «[[Power function]]», |
| − | [[SdPow]], |
+ | «[[SdPow]]», |
| − | [[SuPow]], |
+ | «[[SuPow]]», |
| + | «[[Superfunction]]», |
||
| + | «[[Superfunctions]]», |
||
| + | «[[Superpower]]», |
||
| + | «[[Table of superfunctions]]», |
||
[[Category:Abel equation]] |
[[Category:Abel equation]] |
||
[[Category:Abel function]] |
[[Category:Abel function]] |
||
| + | [[Category:Abelfunction]] |
||
[[Category:Book]] |
[[Category:Book]] |
||
[[Category:Power function]] |
[[Category:Power function]] |
||
Latest revision as of 14:01, 16 August 2025
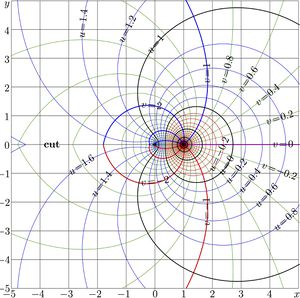

Abelpower appears inverse function of the superpower function.
Abelpower is Abel function for the power function, id est, that of the transfer function \(T(z)\!=\!z^a\) where \(a\) is parameter. Usually, it is assumed, that \(a\!>\!1\).
This article presents a little bit extended spoiler of chapter 4.3 of book «Superfunctions» [1][2] (pages 43-45); some relevant picture are added.
Superpower and Abelpower
For the transfer function \(T(z)\!=\!z^a\), the two superfunctions
\(F(z)=\exp(a^z)\)
and
\(F(z)=\exp(-a^z)\)
are denoted as SuPow and SdPow. For superpower function \(F\), the inverse function \(G\!=\!F^{-1}\) is solution of the Abel equation,
\(G(T(z))=G(z)+1\)
The two solutions (corresponding to the two superfunctions \(F\) above) are:
\(G(z)=\mathrm{AuPow}_a^{-1}(z)=\mathrm{AuPow}_a(z)\) \( =\log_a\!\big(\ln(z)\big)\) \( =\ln\!\big(\ln(z)\big)/\ln(a)\) \( =\ln^2(z)/\ln(a) \)
and
\(G(z)=\mathrm{AdPow}_a^{-1}(z)=\mathrm{AdPow}_a(z)\) \( =\log_a\!\big(\ln(1/z)\big)\) \( =\ln\!\big(\ln(1/z)\big)/\ln(a)\) \( =\ln^2(1/z)/\ln(a)\)
These functions are called Abelpower functions. For \(a\!=\!2\), the explicit plots of these two functions are shown in figure at top. The complex maps of them are shown below with levels of constant real part and levels of constant imaginary part;
\(u\!+\!\mathrm i v=G(x\!+\!\mathrm i y)\)

In the most of the complex plane, values of functions AuPow\(_a\) and AdPow\(_a\) differ for a constant; however, they have different cut lines. In order to compare the systems of cuts for these two functions, the zooming of the central parts of maps for AuPow\(_2\) and AdPow\(_2\) are shown together in the last figure.
Application
Abelpower function shows behaviour, similar to those for other abelfunctions, (see Table of superfunctions), that cannot be expressed as elementary functions.
So, the primary application of the superpower and abelpower functions is testing, tracing of general algorithms for evaluation of superfunctions and abelfunctions. Superpower and abelpower are easy to evaluate through their explicit representations; so, the precision of some general method of evaluation is easy to estimate.
Articles about Abelpower function are loaded in TORI as draft of for the special chapter of the Book Superfunctions. Such a chapter is expected to be especially useful for the colleagues who complain that "The formalism of superfunctions is too complicated"
References
- ↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28
- ↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.
Keywords
«Abel function», «Abelfunction», «Abelpower», «AdPow», «AuPow», «Power function», «SdPow», «SuPow», «Superfunction», «Superfunctions», «Superpower», «Table of superfunctions»,
