Difference between revisions of "File:Elutin1a4tori.jpg"
(Importing image file) |
|||
| Line 1: | Line 1: | ||
| + | Iterations of the [[logistic transfer function]] $f(x)=4x(1\!-\!x)$ (shown qith thick black line) $y=f^c(x)$ for $c=$ 0.2, 0.5, 0.8, 1, 1,5 . |
||
| − | Importing image file |
||
| + | |||
| + | Function $f$ is iterated $c$ times; however, the number $c$ of iterations has no need to be integer. |
||
| + | |||
| + | This pic was generated with the "universal" algorithm that evaluates the iterations of more general function |
||
| + | $f_u(x)=u~x~ (1\!-\!x)$; see |
||
| + | <ref name="logistic"> |
||
| + | http://www.springerlink.com/content/u712vtp4122544x4/ D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98. |
||
| + | </ref>. Namely for $u\!=\!4$, the iterates can be expressed through the elementary function, |
||
| + | and such a plot can be generated, for example, in [[Mathematica]] with very simple code: |
||
| + | F[c_, z_] = 1/2 (1 - Cos[2^c ArcCos[1 - 2 z]]) |
||
| + | Plot[{F[1.5, x], F[1, x], F[.8, x], F[.5, x], F[.2, x]}, {x, 0, 1}] |
||
| + | In order to keep the code short, the colors are not adjusted. |
||
| + | The representation above can be obtained from the representation of the [[superfunction]] $F$ and the [[Abel function]] $G$: |
||
| + | : $f^c(z)=F(c+G(z))$ |
||
| + | at |
||
| + | : $F(z)= \frac{1}{2}(1−\cos(2z))$ |
||
| + | : $G(z)=F^{-1}(z)=\log_2(\arccos(1\!−\!2z))$ |
||
| + | |||
| + | As an exercise, one may check the property $f^{c+d}(z)=f^c(f^d(z))$. |
||
| + | |||
| + | More superfunctions represented through [[elementary function]]s can be found in |
||
| + | <ref name="factorial"> |
||
| + | http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1 D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. |
||
| + | </ref>. |
||
| + | |||
| + | <b>Copyleft</b> 2011 by Dmitrii Kouznetsov. |
||
| + | The free use is allowed. |
||
| + | |||
| + | ==References== |
||
| + | <references/> |
||
| + | |||
| + | [[Category:Mathematical functions]] |
||
| + | [[Category:Graphivs]] |
||
| + | [[Category:Logistic sequence]] |
||
| + | [[Category:Superfuncitons]] |
||
Latest revision as of 09:38, 21 June 2013
Iterations of the logistic transfer function $f(x)=4x(1\!-\!x)$ (shown qith thick black line) $y=f^c(x)$ for $c=$ 0.2, 0.5, 0.8, 1, 1,5 .
Function $f$ is iterated $c$ times; however, the number $c$ of iterations has no need to be integer.
This pic was generated with the "universal" algorithm that evaluates the iterations of more general function $f_u(x)=u~x~ (1\!-\!x)$; see [1]. Namely for $u\!=\!4$, the iterates can be expressed through the elementary function, and such a plot can be generated, for example, in Mathematica with very simple code:
F[c_, z_] = 1/2 (1 - Cos[2^c ArcCos[1 - 2 z]])
Plot[{F[1.5, x], F[1, x], F[.8, x], F[.5, x], F[.2, x]}, {x, 0, 1}]
In order to keep the code short, the colors are not adjusted. The representation above can be obtained from the representation of the superfunction $F$ and the Abel function $G$:
- $f^c(z)=F(c+G(z))$
at
- $F(z)= \frac{1}{2}(1−\cos(2z))$
- $G(z)=F^{-1}(z)=\log_2(\arccos(1\!−\!2z))$
As an exercise, one may check the property $f^{c+d}(z)=f^c(f^d(z))$.
More superfunctions represented through elementary functions can be found in [2].
Copyleft 2011 by Dmitrii Kouznetsov. The free use is allowed.
References
- ↑ http://www.springerlink.com/content/u712vtp4122544x4/ D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98.
- ↑ http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1 D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 | 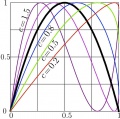 | 922 × 914 (62 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
There are no pages that use this file.