Difference between revisions of "File:ShellThronRegionPaulsen2.png"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| + | [[Shell-Thron region]] in the complex plane (inside the loop). |
||
| + | |||
| + | Figure 1 from publication by [[William Harold Paulsen]], 2019 |
||
| + | <ref> |
||
| + | https://www.researchgate.net/publication/325532999_Tetration_for_complex_bases <br> |
||
| + | https://link.springer.com/article/10.1007/s10444-018-9615-7 |
||
| + | [[William Harold Paulsen]]. Tetration for complex bases. |
||
| + | Advances in Computational Mathematics, volume 45, pages 243–267(2019) |
||
| + | Abstract |
||
| + | In this paper we will consider the tetration, defined by the equation \( F(z+1)= b^F(z)\) in the complex plane with \( F(0)=1\), for the case where \(b\) is complex. A previous paper determined conditions for a unique solution the case where \( b \) is real and \(b>e^{1/e}\). |
||
| + | In this paper we extend these results to find conditions which determine a unique solution for complex bases. We also develop iteration methods for numerically approximating the function F(z), both for bases inside and outside the Shell-Thron region. .. |
||
| + | We say that the base \(b\) is in the [[Shell-Thron region]] if the sequence of values |
||
| + | \( \{ b, b^b, b^{b^b}, b^{b^{b^b}}, ... \}\) converge to a finite [[fixed point]]. |
||
| + | .. |
||
| + | </ref>: |
||
| + | |||
| + | We say that the base \(b\) is in the [[Shell-Thron region]] if the sequence of values |
||
| + | |||
| + | \( \{ b, b^b, b^{b^b}, b^{b^{b^b}}, ... \}\) |
||
| + | |||
| + | converge to a finite [[fixed point]]. |
||
| + | |||
| + | ==References== |
||
| + | <references/> |
||
| + | |||
| + | [[Category:Exp]] |
||
| + | [[Category:Iterate]] |
||
| + | [[Category:Shell-Thron region]] |
||
| + | [[Category:Tetration]] |
||
| + | [[Category:William Paulsen]] |
||
Latest revision as of 06:51, 13 July 2020
Shell-Thron region in the complex plane (inside the loop).
Figure 1 from publication by William Harold Paulsen, 2019 [1]:
We say that the base \(b\) is in the Shell-Thron region if the sequence of values
\( \{ b, b^b, b^{b^b}, b^{b^{b^b}}, ... \}\)
converge to a finite fixed point.
References
- ↑
https://www.researchgate.net/publication/325532999_Tetration_for_complex_bases
https://link.springer.com/article/10.1007/s10444-018-9615-7 William Harold Paulsen. Tetration for complex bases. Advances in Computational Mathematics, volume 45, pages 243–267(2019) Abstract In this paper we will consider the tetration, defined by the equation \( F(z+1)= b^F(z)\) in the complex plane with \( F(0)=1\), for the case where \(b\) is complex. A previous paper determined conditions for a unique solution the case where \( b \) is real and \(b>e^{1/e}\). In this paper we extend these results to find conditions which determine a unique solution for complex bases. We also develop iteration methods for numerically approximating the function F(z), both for bases inside and outside the Shell-Thron region. .. We say that the base \(b\) is in the Shell-Thron region if the sequence of values \( \{ b, b^b, b^{b^b}, b^{b^{b^b}}, ... \}\) converge to a finite fixed point. ..
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:50, 13 July 2020 | 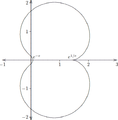 | 569 × 580 (16 KB) | T (talk | contribs) |
You cannot overwrite this file.
File usage
The following page uses this file: