Difference between revisions of "File:Vladi08.jpg"
($ -> \( ; description ; refs ; pre ; keywords) |
|||
| Line 1: | Line 1: | ||
| + | {{oq|Vladi08.jpg|Vladi08.jpg (787 × 375 pixels, file size: 117 KB, MIME type: image/jpeg)}} |
||
| ⚫ | |||
| + | |||
| + | Fig.14.11 from page 200 of book «[[Superfunctions]]» <ref> |
||
| + | https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862 <br> |
||
| + | https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3 <br> |
||
| + | https://mizugadro.mydns.jp/BOOK/468.pdf <br> |
||
| + | Dmitrii Kouznetsov. [[Superfunctions]]. [[Lambert Academic Publishing]], 2020. |
||
| + | </ref>, 2020 |
||
| + | |||
| + | |||
| ⚫ | |||
The similar map at the right hand side represents the comparison to the similar representation through the Cauchi integral, but the contour of integration is displaced for 1/2 to the left. |
The similar map at the right hand side represents the comparison to the similar representation through the Cauchi integral, but the contour of integration is displaced for 1/2 to the left. |
||
| − | Levels |
+ | Levels \(D=\mathrm{const}\) are drawn with step 2, but the exception is dome for level \(D=1\), this level is drawn with thick lines. |
| − | + | \(\displaystyle |
|
{\rm fse}(z)=\left\{ \begin{array}{ccrcccr} |
{\rm fse}(z)=\left\{ \begin{array}{ccrcccr} |
||
{\rm fima}(z) &,& 4.5& \!<\! &\Im(z) \\ |
{\rm fima}(z) &,& 4.5& \!<\! &\Im(z) \\ |
||
| Line 13: | Line 23: | ||
{\rm fima}(z^{*})^{*} &,& & &\Im(z) &\!<\!&\!\! -4.5 |
{\rm fima}(z^{*})^{*} &,& & &\Im(z) &\!<\!&\!\! -4.5 |
||
\end{array} |
\end{array} |
||
| − | \right. |
+ | \right.\) |
Mnemonics for the name of the approximation: Fast Super Exponent. |
Mnemonics for the name of the approximation: Fast Super Exponent. |
||
| Line 19: | Line 29: | ||
The agreement plotted is |
The agreement plotted is |
||
| − | + | \(\displaystyle |
|
D=D_{8}(z)=-\lg\left( \frac |
D=D_{8}(z)=-\lg\left( \frac |
||
{|\mathrm{fse}(z)-F_{4}(z)|} |
{|\mathrm{fse}(z)-F_{4}(z)|} |
||
{|\mathrm{fse}(z)|+|F_{4}(z)|} |
{|\mathrm{fse}(z)|+|F_{4}(z)|} |
||
\right) |
\right) |
||
| + | \) |
||
| − | $ |
||
| − | where |
+ | where \(F_4\) denotes the 4th [[ackermann]], id set, [[natural tetration]] evaluated through the [[Cauchi integral]] |
| − | <ref> |
+ | <ref name="analuxp"> |
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html <br> |
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html <br> |
||
| − | http:// |
+ | http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf |
| ⚫ | |||
| − | http://mizugadro.mudns.jp/PAPERS/2009analuxpRepri.pdf |
||
| ⚫ | |||
</ref>. |
</ref>. |
||
| − | + | The same image is used also as Рис.14.11 in the Russian version «[[Суперфункции]]»<ref> |
|
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br> |
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br> |
||
| − | http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br> |
||
http://mizugadro.mydns.jp/BOOK/202.pdf |
http://mizugadro.mydns.jp/BOOK/202.pdf |
||
| − | Д.Кузнецов. Суперфункции. [[Lambert Academic Publishing]], 2014. |
+ | Д.Кузнецов. [[Суперфункции]]. [[Lambert Academic Publishing]], 2014. |
| + | </ref>, 2014. |
||
| − | </ref>; the English version is in preparation in 2015. |
||
First time published in the [[Vladikavkaz Matehmatical Journal]] |
First time published in the [[Vladikavkaz Matehmatical Journal]] |
||
<ref> |
<ref> |
||
http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf |
http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf |
||
| − | D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. |
+ | D.Kouznetsov. Superexponential as special function. [[Vladikavkaz Mathematical Journal]], 2010, v.12, issue 2, p.31-45. |
Figure 8. |
Figure 8. |
||
| − | </ref>. |
+ | </ref>, 2010. |
| + | The figure suggests that the fast implementation [[fsexp.cin]] with elementary functions happens to |
||
| ⚫ | |||
| + | provide a little bit better precision that the initial implementation of [[natural tetration]] through the [[Cauchi integral]] <ref name="analuxp"/> (2009). |
||
| − | <references/> |
||
==[[C++]] generator of the first picture== |
==[[C++]] generator of the first picture== |
||
| − | [[Fsexp.cin]], |
+ | /* [[Fsexp.cin]], |
[[ado.cin]], |
[[ado.cin]], |
||
[[conto.cin]], |
[[conto.cin]], |
||
[[plodi.cin]] |
[[plodi.cin]] |
||
| − | should be loaded in order to compile the code below |
+ | should be loaded in order to compile the code below */ |
| + | <pre> |
||
| − | |||
| − | <poem><nomathjax><nowiki> |
||
| − | |||
#include <math.h> |
#include <math.h> |
||
#include <stdio.h> |
#include <stdio.h> |
||
| Line 124: | Line 130: | ||
} |
} |
||
| + | </pre> |
||
| − | </nowiki></nomathjax></poem> |
||
==[[C++]] generator of the second picture== |
==[[C++]] generator of the second picture== |
||
| − | [[vladif5c.cin]] also should be loaded |
+ | /* [[vladif5c.cin]] also should be also loaded */ |
| + | <pre> |
||
| − | |||
| − | <poem><nomathjax><nowiki> |
||
| − | |||
#include <math.h> |
#include <math.h> |
||
#include <stdio.h> |
#include <stdio.h> |
||
| Line 196: | Line 200: | ||
//getchar(); system("killall Preview"); |
//getchar(); system("killall Preview"); |
||
} |
} |
||
| + | </pre> |
||
| − | </nowiki></nomathjax></poem> |
||
| − | |||
==[[Latex]] combiner== |
==[[Latex]] combiner== |
||
| + | <pre> |
||
| − | <poem><nomathjax><nowiki> |
||
\documentclass[12pt]{article} |
\documentclass[12pt]{article} |
||
\usepackage{graphicx} |
\usepackage{graphicx} |
||
| Line 254: | Line 257: | ||
\put(68,20){\sx{.5}{$D\!<\!1$}} |
\put(68,20){\sx{.5}{$D\!<\!1$}} |
||
\end{picture}} |
\end{picture}} |
||
| − | |||
\end{document} |
\end{document} |
||
| + | </pre> |
||
| − | </nowiki></nomathjax></poem> |
||
| ⚫ | |||
| + | {{ref}} |
||
| + | {{fer}} |
||
| + | ==Keywords== |
||
| ⚫ | |||
| + | «[[Approximation]]», |
||
| + | «[[Natural tetration]]», |
||
| + | «[[Superfunction]]», |
||
| + | «[[Superfunctions]]», |
||
| ⚫ | |||
[[Category:Agreement]] |
[[Category:Agreement]] |
||
| + | [[Category:Approximation]] |
||
[[Category:Book]] |
[[Category:Book]] |
||
| ⚫ | |||
[[Category:BookMap]] |
[[Category:BookMap]] |
||
| ⚫ | |||
[[Category:C++]] |
[[Category:C++]] |
||
[[Category:Latex]] |
[[Category:Latex]] |
||
| + | [[Category:Natural tetration]] |
||
| + | [[Category:Superfunction]] |
||
| + | [[Category:Superfunctions]] |
||
| + | [[Category:Test]] |
||
| + | [[Category:Tetration]] |
||
Latest revision as of 20:59, 17 December 2025
Fig.14.11 from page 200 of book «Superfunctions» [1], 2020
Agreement of approximations of natural tetration by elementary functions with the original representation through the Cauchi integral is shown in the left hand side map.
The similar map at the right hand side represents the comparison to the similar representation through the Cauchi integral, but the contour of integration is displaced for 1/2 to the left.
Levels \(D=\mathrm{const}\) are drawn with step 2, but the exception is dome for level \(D=1\), this level is drawn with thick lines.
\(\displaystyle {\rm fse}(z)=\left\{ \begin{array}{ccrcccr} {\rm fima}(z) &,& 4.5& \!<\! &\Im(z) \\ {\rm tai}(z) &,& 1.5& \!<\! &\Im(z) &\!\le\!& 4.5 \\ {\rm maclo}(z) &,& -1.5& \le &\Im(z) &\!\le\!& 1.5 \\ {\rm tai}(z^{*})^{*} &,& -4.5& \le &\Im(z) &\!<\!&\!\! -1.5 \\ {\rm fima}(z^{*})^{*} &,& & &\Im(z) &\!<\!&\!\! -4.5 \end{array} \right.\)
Mnemonics for the name of the approximation: Fast Super Exponent.
The agreement plotted is
\(\displaystyle D=D_{8}(z)=-\lg\left( \frac {|\mathrm{fse}(z)-F_{4}(z)|} {|\mathrm{fse}(z)|+|F_{4}(z)|} \right) \)
where \(F_4\) denotes the 4th ackermann, id set, natural tetration evaluated through the Cauchi integral [2].
The same image is used also as Рис.14.11 in the Russian version «Суперфункции»[3], 2014.
First time published in the Vladikavkaz Matehmatical Journal [4], 2010.
The figure suggests that the fast implementation fsexp.cin with elementary functions happens to provide a little bit better precision that the initial implementation of natural tetration through the Cauchi integral [2] (2009).
C++ generator of the first picture
/* Fsexp.cin, ado.cin, conto.cin, plodi.cin should be loaded in order to compile the code below */
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
//#include "superex.cin"
#include "fsexp.cin"
#include "f4natu.cin"
//z_type FSEXP(z_type z){DB y=Im(z);
z_type fsexp(z_type z){DB y=Im(z);
if(y> 4.5) return fima(z);
if(y> 1.5) return tai3(z);
if(y>-1.5) return maclo(z);
if(y>-4.5) return conj(tai3(conj(z)));
return conj(fima(conj(z)));
}
//#include "superlo.cin"
#include "conto.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
z_type Zo=z_type(.31813150520476413, 1.3372357014306895);
z_type Zc=z_type(.31813150520476413,-1.3372357014306895);
int M=100,M1=M+1;
int N=101,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
//FILE *o;o=fopen("figcf4small.eps","w");ado(o,0,0,82,82);
FILE *o;o=fopen("vladi08a.eps","w");ado(o,82,82);
fprintf(o,"41 11 translate\n 10 10 scale\n");
DO(m,M1) X[m]=-4.+.08*(m-.5);
DO(n,N1) Y[n]=-1.+.08*(n-.5);
for(m=-3;m<4;m++) { if(m==0){M(m,-0.1)L(m,6.1)} else {M(m,0)L(m,6)} }
for(n=0;n<7;n++) { M( -3,n)L(3,n)}
fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; printf("run at x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
c=fsexp(z);
d=F4natu(z);
p=abs(c-d);///(abs(c)+abs(d));
p=-log(p)/log(10.);
// p=Re(c); q=Im(c);
if(p>-999 && p<999 && fabs(p)> 1.e-8 && fabs(p-1.)>1.e-8) g[m*N1+n]=p;
// if(q>-999 && q<999 && fabs(q)> 1.e-8) f[m*N1+n]=q;
}}
#include"plodi.cin"
//M(-2,0)L(-3.1,0) fprintf(o,".04 W 0 0 0 RGB [.1 .1] 1 setdash S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
// system( "gv fig08a.eps");
system("epstopdf vladi08a.eps");
system( "open vladi08a.pdf"); // for linux
// getchar(); system("killall Preview");// for macintosh
}
C++ generator of the second picture
/* vladif5c.cin also should be also loaded */
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
//#include "superex.cin"
#include "fsexp.cin"
//#include "f4natu.cin"
#include "vladif5c.cin"
//z_type FSEXP(z_type z){DB y=Im(z);
z_type fsexp(z_type z){DB y=Im(z);
if(y> 4.5) return fima(z);
if(y> 1.5) return tai3(z);
if(y>-1.5) return maclo(z);
if(y>-4.5) return conj(tai3(conj(z)));
return conj(fima(conj(z)));
}
//#include "superlo.cin"
#include "conto.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
z_type Zo=z_type(.31813150520476413, 1.3372357014306895);
z_type Zc=z_type(.31813150520476413,-1.3372357014306895);
int M=100,M1=M+1;
int N=101,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
//FILE *o;o=fopen("figcf5small.eps","w");ado(o,0,0,82,82);
FILE *o;o=fopen("vladi08b.eps","w");ado(o,82,82);
fprintf(o,"41 11 translate\n 10 10 scale\n");
DO(m,M1)X[m]=-4.+.08*(m-.5);
DO(n,N1)Y[n]=-1.+.08*(n-.5);
for(m=-3;m<4;m++) { if(m==0){M(m,-0.1)L(m,6.1)} else {M(m,0)L(m,6)} }
for(n= 0;n<7;n++) { M( -3,n)L(3,n)}
fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; printf("run at x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
c=fsexp(z);
d=F5(z);
p=abs(c-d);///(abs(c)+abs(d));
p=-log(p)/log(10.);
// p=Re(c); q=Im(c);
if(p>-999 && p<999 && fabs(p)> 1.e-8 && fabs(p-1.)>1.e-8) g[m*N1+n]=p;
// if(q>-999 && q<999 && fabs(q)> 1.e-8) f[m*N1+n]=q;
}}
#include"plodi.cin"
//M(-2,0)L(-3.1,0) fprintf(o,".04 W 0 0 0 RGB [.1 .1] 1 setdash S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf vladi08b.eps");
system( "open vladi08b.pdf");//linux
//getchar(); system("killall Preview");
}
Latex combiner
\documentclass[12pt]{article}
\usepackage{graphicx}
\usepackage{rotating}
\usepackage{geometry}
\paperwidth 378px
%\paperheight 134px
\paperheight 180px
\topmargin -104pt
\oddsidemargin -94pt
\pagestyle{empty}
\begin{document}
\newcommand \ing {\includegraphics}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\sx{2.2}{\begin{picture}(90,80)
%\put(0,0){\includegraphics{figsexpF4}}
%\put(0,0){\includegraphics{figcf4small}}
\put(0,0){\includegraphics{vladi08a}}
\put(5,68){\sx{.45}{$\Im(z)$}}
\put(7,59){\sx{.5}{$5$}}
\put(7,49){\sx{.5}{$4$}}
\put(7,39){\sx{.5}{$3$}}
\put(7,29){\sx{.5}{$2$}}
\put(7,19){\sx{.5}{$1$}}
\put(7, 9){\sx{.5}{$0$}}
\put(70 , 6){\sx{.45}{$\Re(z)$}}
\put(60 , 6){\sx{.5}{$2$}}
\put(40 , 6){\sx{.5}{$0$}}
\put(17 ,6){\sx{.5}{$-\!2$}}
\put(25,62){\sx{.5}{$D\!>\!14$}}
\put(55,60){\sx{.5}{$12\!<\!D\!<\!14$}}
\put(68,20){\sx{.5}{$D\!<\!1$}}
\end{picture}}
\sx{2.2}{\begin{picture}(80,80)
%\put(0,0){\includegraphics{figsexpF5}}
%\put(0,0){\includegraphics{figcf5small}}
\put(0,0){\includegraphics{vladi08b}}
\put(5,68){\sx{.45}{$\Im(z)$}}
\put(7,59){\sx{.5}{$5$}}
\put(7,49){\sx{.5}{$4$}}
\put(7,39){\sx{.5}{$3$}}
\put(7,29){\sx{.5}{$2$}}
\put(7,19){\sx{.5}{$1$}}
\put(7, 9){\sx{.5}{$0$}}
\put(70 , 6){\sx{.45}{$\Re(z)$}}
\put(60 , 6){\sx{.5}{$2$}}
\put(40 , 6){\sx{.5}{$0$}}
\put(17 ,6){\sx{.5}{$-\!2$}}
\put(31,56){\sx{.5}{$D\!>\!14$}}
\put(68,20){\sx{.5}{$D\!<\!1$}}
\end{picture}}
\end{document}
Refereces
- ↑
https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862
https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3
https://mizugadro.mydns.jp/BOOK/468.pdf
Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020. - ↑ 2.0 2.1
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. - ↑
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014. - ↑ http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. Figure 8.
Keywords
«Agreement», «Approximation», «Natural tetration», «Superfunction», «Superfunctions», «Tetration»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:14, 1 December 2018 | 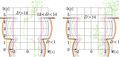 | 787 × 375 (117 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
There are no pages that use this file.