Difference between revisions of "Nemtsov function"
m (some cosmetics) |
|||
| (16 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{top}} |
||
| − | [[File:Nemplot.jpg|100px|thumb|Fig.1. $y=\mathrm{Nem}_q(x)$ versus $x$ for various $q$]] |
||
| + | <div class="thumb tright" style="float:right; margin:-76px 0px 0px 8px; line-height:2px; background-color:#fff"> |
||
| − | [[File:Nem100map.jpg|140px|thumb|Fig.2. $u\!+\!\mathrm i v=\mathrm{Nem}_0(x\!+\!\mathrm i y)$]] |
||
| + | {{pic|Nemplot.jpg|120px}}<small><center>\(y=\mathrm{nem}_q(x)\)</center></small> |
||
| − | [[File:Nem120map.jpg|140px|thumb|Fig.3. $u\!+\!\mathrm i v=\mathrm{Nem}_2(x\!+\!\mathrm i y)$]] |
||
| + | </div> |
||
| − | [[File:Nembraplot.jpg|100px|thumb|Fig.4. $x\!+\!\mathrm i y= \mathrm{NemBra}(q)$]] |
||
| − | [[File:Nembrant.jpg|100px|thumb|Fig.5. $x\!+\!\mathrm i y= \mathrm{NemBran}(q)$]] |
||
| − | [[File:Arqnem100map.jpg|160px|thumb|Fig.6. $u\!+\!\mathrm i v=\mathrm{ArqNem}_0(x\!+\!\mathrm i y)$]] |
||
| − | [[File:Arqnem120map.jpg|160px|thumb|Fig.7. $u\!+\!\mathrm i v=\mathrm{ArqNem}_2(x\!+\!\mathrm i y)$]] |
||
| + | <div class="thumb tright" style="float:right; margin:0px 0px 4px 8px; width:408px"> |
||
| − | [[Nemtsov function]] is polynomial of special kind, suggested as an example of a [[transfer function]] |
||
| + | {{pic|Nem0map.jpg|200px}} {{pic|ArqNem0map.jpg|200px}} |
||
| − | for the book [[Superfunctions]]. |
||
| + | {{pic|Nem2map.jpg|200px}} {{pic|ArqNem2map.jpg|200px}} |
||
| + | <small><center>Complex maps: \(u+\mathrm i v=f(x+\mathrm i y)\) for \(f=\mathrm{nem}_0\), \(f=\mathrm{ArqNem}_0\) (top) and for \(f=\mathrm{nem}_2\), \(f=\mathrm{ArqNem}_2\) (bottom)</center></small> |
||
| + | </div> |
||
| + | The [[Nemtsov function]] is a special kind of polynomial, suggested as an example of a [[transfer function]] in the book «[[Superfunctions]]» <ref name="book"> |
||
| − | The [[Nemtsov function]] $y=\mathrm{Nem}_q(x)= x+x^3+q x^4$ |
||
| + | https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862 <br> |
||
| − | is shown in figure at right versis $x$ for various $q\!\ge\!0$. |
||
| + | https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3 <br> |
||
| + | https://mizugadro.mydns.jp/BOOK/468.pdf <br> |
||
| + | Dmitrii Kouznetsov. ''Superfunctions''. [[Lambert Academic Publishing]], 2020. |
||
| + | </ref>. |
||
| + | The description is also available as the [[Mizugadro Preprint]] <ref> |
||
| + | https://mizugadro.mydns.jp/PAPERS/2016nemtsov.pdf <br> |
||
| + | Dmitrii Kouznetsov. ''Nemtsov function and its iterates''. [[Mizugadro Preprint]], 2016. |
||
| + | </ref>. |
||
| − | [[ |
+ | The [[Nemtsov function]] \(y=\mathrm{nem}_q(x)= x+x^3+q\,x^4\) is shown in the figure at right for various \(q\ge 0\). |
| − | lines $v\!=\!\mathrm{const}$ assuming that $u\!+\!\mathrm i v=\mathrm{Nem}_0(x\!+\!\mathrm i y)$ . |
||
| + | [[Complex map]]s of \(\mathrm{nem}_q\) are shown in the left column of the figure below. |
||
| − | ==Definition== |
||
| + | The right column shows similar maps for the inverse function \(\mathrm{ArqNem}_q=\mathrm{nem}_q^{-1}\). |
||
| + | This article describes the Nemtsov function and its related functions: |
||
| − | Let $q$ be non–negative real parameter. Then, Nemtsov Function $\mathrm{Nem}$ is defined for complex argument $z$ as follows: |
||
| + | the inverse function [[ArqNem]], |
||
| + | the [[superfunction]] [[SuNem]], and |
||
| + | the [[Abel function]] [[AuNem]]. |
||
| + | == Motivation == |
||
| − | (1)$~ ~ ~ ~ ~ ~ \mathrm{Nem}_q(z)= z+z^3+q z^4$ |
||
| + | The [[Nemtsov function]] serves as an example of a real-holomorphic [[transfer function]] with a real [[fixed point]], where the usual [[regular iteration]] method for constructing a [[superfunction]] cannot be applied directly. |
||
| − | ==Notations== |
||
| + | The editor did not find any simpler example of this type other than this specific fourth-order polynomial. |
||
| + | The function was introduced as an attempt to construct an “exotic’’ [[transfer function]] for which a growing real-holomorphic [[superfunction]] could not be produced by the usual methods appearing in the «[[Table of superfunctions]]». |
||
| − | For Function $~ \mathrm{Nem}_q~$ by equation (1), at $q\!>\!0$, the algorithms, described in the first edition of the Russian version of the book [[Суперфункции]] cannot be applied "as is", and some modification, generalisation is required. The need of this modification had been revealed 2015.02.27, in the day, when [[Putin killed Nemtsov]]. Since February to July of 2015, no other scientific concept of that murder hat been suggested. Apparently, the total [[corruption]] in Russia does not allow the professional to investigate that case, and that terroristic act caused many publications. This makes name Nemtsov to be a good mark, label on the timeline of Hunan History. |
||
| + | This attempt failed — the [[superfunction]] for the Nemtsov function *can* be constructed, and is described below. |
||
| + | The expansion of the Nemtsov function at its fixed point begins with a linear term whose coefficient is unity. This prevents the use of standard [[regular iteration]] <ref> |
||
| − | For this reason, function $\mathrm{Nem}_q$ by equation (1) is called after the name of Boris Nemtsov. |
||
| + | http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html <br> |
||
| + | https://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf <br> |
||
| + | D. Kouznetsov, H. Trappmann. ''Portrait of the four regular super-exponentials to base sqrt(2)''. ''Mathematics of Computation'', 2010, v.79, p.1727–1756. |
||
| + | </ref>, which works for the exponential to base \(\sqrt{2}\). |
||
| + | The situation is similar to the exponential to base \(\exp(1/\mathrm e)\) <ref name="e1e"> |
||
| − | In this article, properties of the Nemtsov function are considered, and also some properties of the related functions: |
||
| + | http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf <br> |
||
| + | https://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf <br> |
||
| + | H. Trappmann, D. Kouznetsov. ''Computation of the Two Regular Super-Exponentials to base exp(1/e)''. ''Mathematics of Computation'', 81 (2012), 2207–2227. |
||
| + | </ref>, but the Nemtsov function lacks the quadratic term, so the [[exotic iteration]] of <ref name="e1e"/> cannot be used as is. |
||
| + | A closer analogy is the case of the sine function <ref> |
||
| − | Inverse function, denoted with [[ArqNem]], |
||
| + | http://www.pphmj.com/references/8246.htm <br> |
||
| + | https://mizugadro.mydns.jp/PAPERS/2014susin.pdf <br> |
||
| + | Dmitrii Kouznetsov. ''SUPER SIN''. ''Far East Journal of Mathematical Sciences'' 85(2), 219–238 (2014). |
||
| + | </ref>, but sine is antisymmetric, \(\sin(-z)=-\sin(z)\), which simplifies its analysis. |
||
| + | The Nemtsov function for \(q>0\) has no such symmetry, leading initially to doubts whether a superfunction could be constructed. |
||
| + | Eventually, the construction succeeded. |
||
| − | $\mathrm{Nem}_q(\mathrm{ArqNem}_q(z))=z$ |
||
| + | <div class="thumb tright" style="float:right; margin:-4px 0px 4px 8px"> |
||
| − | [[Superfunction]], denoted with [[SuNem]], |
||
| + | {{pic|Boris.jpg|100px}}<small><center>[[Немцов Борис Ефимович|B. Nemtsov]]<ref>http://nemtsov.ru Борис Немцов</ref></center></small></div> |
||
| + | The need for a special name for this function emerged on 2015-02-27, the day when [[Putin killed Nemtsov]]. |
||
| − | $\mathrm{SuNem}_q(z\!+\!1)=\mathrm{Nem}_q(\mathrm{SuNem}_q(z))$ |
||
| + | As of 2025, no other scientific concept attached to that event has appeared. |
||
| + | The total [[corruption]] in Russia <ref name="medvedko"> |
||
| + | http://kremlin.ru/transcripts/1566 <br> |
||
| + | D. Medvedev: ''Corruption in our country has acquired not just a large-scale character; it has become a habitual, everyday phenomenon...'' (2008) |
||
| + | </ref> prevents professional investigation of the crime. |
||
| + | Thus, the family name “Nemtsov’’ serves as a historical timestamp. |
||
| + | By 2025, no better notation for this polynomial has been proposed. |
||
| − | [[Abel function]], denoted with [[SuNem]], |
||
| + | The function symbol is written as lowercase \(\mathrm{nem}\), following the convention for mathematical functions, even though “Nemtsov’’ is a proper name. |
||
| + | Capitalization is used only when distinguishing it from derived functions such as [[ArqNem]], [[AuNem]], and [[SuNem]]. |
||
| + | == Definition and notations == |
||
| − | $\mathrm{SuNem}_q(\mathrm{Nem}_q(z))=\mathrm{SuNem}_q(z)+1$ |
||
| + | Let \(q\ge 0\) be a real parameter. |
||
| − | and the corresponding [[iterate]]s |
||
| + | The [[Nemtsov function]] is defined for complex argument \(z\) by |
||
| + | \[ |
||
| − | $\mathrm{Nem}_q^n(z)=\mathrm{SuNem}_q\big(n+ \mathrm{SuNem}_q(z)\big)$ |
||
| + | \mathrm{nem}_q(z)=z+z^3+q\,z^4 |
||
| + | \tag{1} |
||
| + | \] |
||
| + | For \(q>0\), the algorithms described in the first Russian edition of «[[Суперфункции]]» (2014) |
||
| − | The inverse function is called [[ArqNem]]. This name allows to distinguish it from other inverse functions of the [[Nemtsov function]]. Two other inverse functions are called [[ArcNem]] and [[ArkNem]]. A priori, it had been difficult to guess, that namely [[ArqNem]] happens to be suitable for construction of the corresponding [[Abel function]]; so, all the three versions had been assigned (designated) the different names. These inverse functions have different positions of the cuts of the range of holomorphism. |
||
| + | <ref> |
||
| + | http://mizugadro.mydns.jp/BOOK/202.pdf |
||
| + | Дмитрий Кузнецов. [[Суперфункции]]. [[Lambett Academic Publishing]], 2014. (in Russian) |
||
| + | </ref> cannot be applied in their original form; a small generalization is required. |
||
| + | Thus the function \(\mathrm{nem}_q\) is treated as a [[transfer function]]. |
||
| + | This appears to be the last remaining attempt (as of 2025) to produce a real-holomorphic, growing transfer function whose [[superfunction]] cannot be constructed by methods already known in the literature. |
||
| − | The [[Abel function]] for the Nemtov function is called [[AuNem]], to indicate, that it is constructed by the [[exotic iterates]] at the [[fixed point]] zero, that is maximal (Upper) among the fixed points of the Nemtsov function. |
||
| + | But again, the attempt fails: both the [[superfunction]] [[SuNem]] and the [[Abel function]] [[AuNem]] are constructed using a method similar to that used for the sine function. |
||
| − | While no other iterates of the Nemtsov function are presented no special mark is used to denote |
||
| − | the iterates $\mathrm{Nem}_q^n$. Later, perhaps, one additional subscript $_{\mathrm u}$ will be |
||
| − | added to the notation, in order to distinguish this iterate from other iterates, constructed, for example, using the asymptotic behaviour of the [[Nemtsov function]] (and its iterates) at infinity. |
||
| + | Associated functions: |
||
| − | ==General properties== |
||
| + | [[Inverse function]]: \(\mathrm{ArqNem}_q\), satisfying |
||
| − | For real $q$, the [[Nemtsov function]] is real holomorphic in the whole complex plane; |
||
| + | \[ |
||
| + | \mathrm{nem}_q(\mathrm{ArqNem}_q(z)) = z |
||
| + | \] |
||
| + | [[Superfunction]] \(\mathrm{SuNem}_q\), satisfying |
||
| − | $\mathrm{Nem}_q(z^*)=\mathrm{Nem}_q(z)^*$ |
||
| + | \[ |
||
| + | \mathrm{SuNem}_q(z+1) = \mathrm{nem}_q(\mathrm{SuNem}_q(z)) |
||
| + | \] |
||
| + | [[Abel function]]: \(\mathrm{AuNem}_q=\mathrm{SuNem}_q^{-1}\), satisfying |
||
| − | At least for positive values of the argument, the Nemtsov function grows monotonously. |
||
| + | |||
| − | The monotonous growth has also the inverse function [[ArqNem]], the Abel function [[AuNem]] and the real iterates of the Nemtsov function. |
||
| + | \[ |
||
| + | \mathrm{AuNem}_q(\mathrm{nem}_q(z)) = \mathrm{AuNem}_q(z) + 1 |
||
| + | \] |
||
| + | Several inverse functions exist: [[ArcNem]], [[ArkNem]], and [[ArqNem]]. |
||
| − | As for any non–trivial entire function, the inverse function $\mathrm{ArqNem}_q$ has the branch points. Two of them are complex; and one of them is expressed with function [[NemBran]]; |
||
| + | They differ in branch-cut placement. |
||
| − | at $z=\mathrm{NemBran}(q)$, function $\mathrm{ArqNem}_q(z)$ has infinite derivative. |
||
| + | [[ArqNem]] turns out to be the correct one for defining holomorphic non-integer iterates near the positive real axis; therefore it is adopted as the default inverse. |
||
| + | == Inverse function == |
||
| − | For construction of the inverse function, important are the complex soluitons $A$ of equation $\mathrm{Nem}_q^{\prime}=0$. |
||
| − | One of these solutions is expressed with function [[NemBra]], id est, $A=\mathrm{NemBra}(q)$. Parametric plot of this function is shown in figure 4: |
||
| + | <div class="thumb tright" style="float:right; margin:-32px 0px 200px 2px; width:328px; height:400px; background-color:#fff"> |
||
| − | $x=\mathrm{Re}\big(\mathrm{NemBra}(q)\big)~$ |
||
| + | <p style="margin:0px 0px 0px 9px;line-height:0px; width:200px; background-color:#fff"> {{pic|Nembraplot.jpg|144px}}</p> |
||
| + | <p style="margin:-348px 0px 348px 180px; line-height:0px">{{pic|Nembrant.jpg|144px}}</p> |
||
| + | <p style="margin:-342px 0px 0px 24px;"><small><center> \(x\!+\!\mathrm i y\!=\!\mathrm{NemBra}(q) ~\) and \(~ x\!+\!\mathrm i y\!=\!\mathrm{NemBran}(q)\)</center></small></p> |
||
| + | </div> |
||
| + | To construct the inverse function in the complex plane, one must locate the saddle points and choose suitable branch cuts. |
||
| − | $y=\mathrm{Im}\big(\mathrm{NemBra}(q)\big)~$ |
||
| + | In the complex maps shown previously, the yellow lines indicate the branch cuts for functions \(\mathrm{ArqNem}_0\) and \(\mathrm{ArqNem}_2\). |
||
| + | These lines connect the two complex branch points of \(\mathrm{ArqNem}_q\). |
||
| + | For real \(q\), the Nemtsov function is real-holomorphic in the whole complex plane: |
||
| − | For positive $q$, both real and imaginary parts of the branchpoint are significantly smaller than unity. |
||
| + | \[ |
||
| − | ==Inverse function== |
||
| + | \mathrm{nem}_q(z^{*}) = \mathrm{nem}_q(z)^{*}. |
||
| + | \] |
||
| + | For positive real arguments, the function grows monotonically. |
||
| − | The [[Nemtsov function]] has various inverse functions, as equation |
||
| + | This monotonicity is inherited by its inverse \(\mathrm{ArqNem}_q\), its Abel function \(\mathrm{AuNem}_q\), and its real iterates. |
||
| + | The inverse function \(\mathrm{ArqNem}_q\) has complex [[branch point]]s. |
||
| − | $\mathrm{Nem}_q(A)=z$ |
||
| + | One of them is described explicitly by the function [[NemBran]]. |
||
| + | At \(z=\mathrm{NemBran}(q)\), the derivative of \(\mathrm{ArqNem}_q(z)\) becomes infinite. |
||
| + | The branch points arise from the complex solutions \(A\) of the equation |
||
| − | has many solutions $A$ ; there are three solutions for $q\!=\!0$ and four for $q\!\ne\!0$. The holomorphic inverse function unavoidably has the cut lines. |
||
| − | The appropriate choice of these cut lines happens to be non–trivial problem. |
||
| + | \[ |
||
| − | For construction of the [[Abel function]], denoted as [[AuNem]], the special inverse function [[ArqNem]] of the [[Nemtsov function]] is chosen. For function [[ArqNem]], the cut lines are chosen in the following way. |
||
| + | \mathrm{nem}_q'(A) = 0. |
||
| − | One cut line goes along the negative part of the real axis from $-\infty$ to zero. |
||
| + | \] |
||
| − | Two other cut lines go straightly from zero to the complex branchpoints $Z_o$ of the inverse function. |
||
| − | These brach points can be expressed in the following way: |
||
| + | One such solution is denoted \(\mathrm{NemBra}(q)\), and its image |
||
| − | $Z_{\mathrm o}=\mathrm{Nem}_q(z_{\mathrm o})$ |
||
| + | \[ |
||
| − | where $z_{\mathrm o}=\mathrm{NemBran}(q)$ is solution of equation |
||
| + | \mathrm{NemBran}(q) = \mathrm{nem}_q(\mathrm{NemBra}(q)). |
||
| + | \] |
||
| + | For positive \(q\), both real and imaginary parts of \(\mathrm{NemBra}(q)\) and \(\mathrm{NemBran}(q)\) are small (well below unity). |
||
| − | $\mathrm{Nem}_q^{\prime}( z_{\mathrm o})=0$ |
||
| + | Once \(\mathrm{NemBra}\) is implemented, an efficient algorithm for inverse functions becomes possible. |
||
| − | The following relation takes place: |
||
| + | Three versions—[[ArcNem]], [[ArkNem]], and [[ArqNem]]—differ only in branch-cut structure. |
||
| + | [[ArqNem]] is best suited for constructing holomorphic non-integer iterates near the positive real axis. |
||
| + | The [[C++]] implementation of \(\mathrm{ArqNem}_q\) is available as [[arqnem.cin]]. |
||
| − | $\mathrm{NemBran}(q)=\mathrm{Nem}_q\big(\mathrm{NemBra}(q)\big)$ |
||
| + | Parameter \(q\) is stored in the global variable `Q`. |
||
| + | Before evaluating \(\mathrm{ArqNem}_q(z)\), the corresponding branch point must be computed via [[nembran.cin]] and stored in global variables (real and imaginary parts). |
||
| + | == Superfunction == |
||
| − | [[Parametric plot]] of function [[NemBran]] is shown in figure 5: |
||
| + | <div class="thumb tleft" style="float:left; margin:-4px 12px 8px -4px; background-color:#fff"> |
||
| − | $x=\mathrm{Re}\big(\mathrm{NemBran}(q)\big)~$, |
||
| + | {{pic|Sunemplo4t.jpg|180px}}<small><center>\(y=\mathrm{SuNem}_{q}(x)\) for various \(q\)</center></small> |
||
| + | </div> |
||
| + | <div class="thumb tright" style="float:right; margin:-36px 0px 0px 2px"> |
||
| − | $y=\mathrm{Im}\big(\mathrm{NemBran}(q)\big)~$ |
||
| + | {{pic|Sunem0map6.jpg|200px}}<small><center>\(u+\mathrm i v=\mathrm{SuNem}_0(x+\mathrm i y)\)</center></small> |
||
| + | <!-- |
||
| + | {{pic|Sunem1map6.jpg|200px}}<small><center>\(u+\mathrm i v=\mathrm{SuNem}_1(x+\mathrm i y)\)</center></small> |
||
| + | !--> |
||
| + | {{pic|Sunem2map6.jpg|200px}}<small><center>\(u+\mathrm i v=\mathrm{SuNem}_2(x+\mathrm i y)\)</center></small> |
||
| − | At small values of the argument, the [[Nemtsov function]] looks similar to the [[identity function]]; so, the parametric plot of function [[NemBran]] in figure 5 looks similar to that of function [[NemBra]] in figure 4. |
||
| + | </div> |
||
| + | For the transfer function \(\mathrm{nem}_q\), the [[superfunction]] \(\mathrm{SuNem}_q\) is the real-holomorphic solution \(F\) of the transfer equation |
||
| − | [[Complex map]] of function [[ArqNem]] is shown in figure 6 for $q\!=\!0~$ and in figure 7 for $q\!=\!2~$: |
||
| + | \[ |
||
| − | $u\!+\!\mathrm i v= \mathrm{ArqNem}_q(x\!+\!\mathrm i y)$ |
||
| + | F(z+1) = \mathrm{nem}_q(F(z)), |
||
| + | \] |
||
| + | with the asymptotic condition at \(-\infty\): |
||
| − | The complex double implementation of function [[ArqNem]] is loaded as [[arqnem.cin]] ; parameter $q$ is storem in the global variable $Q$. Before evaluation of $\mathrm{ArqNem}_q$ of complex argument, the complex branch point should be evaluated with routine [[nembran.cin]] and stored in the global variables tr and ti; in the version from year 2015, the real and imaginary parts of the branch point are stored as two global variables. |
||
| − | At any change of parameter $q$, these values should be recalculated. |
||
| + | \[ |
||
| − | ==Superfunction== |
||
| + | F(z) = \frac{1}{\sqrt{-2z}} |
||
| − | [[File:Sunemplo4t.jpg|180px|left|thumb|$y\!=\!\mathrm{SuNem}_{q}(x)$ for various $q$]] |
||
| + | \left( 1 - \frac{q}{\sqrt{-2z}} |
||
| − | <!-- |
||
| + | + O\!\left( \frac{\ln(-z)}{z} \right) |
||
| − | [[File:Sunemplot.jpg|200px|left| thumb|$y\!=\!\mathrm{SuNem}_q(x)$ for |
||
| + | \right), |
||
| − | $q\!=\!0$, |
||
| + | \qquad z\to -\infty. |
||
| − | $q\!=\!1$ and for |
||
| + | \] |
||
| − | $q\!=\!2$]]!--> |
||
| + | |||
| − | [[File:Sunem0map6.jpg|200px|thumb|$u\!+\!\mathrm i v=\mathrm{SuNem}_0(x\!+\!\mathrm i y)$]] |
||
| + | To fully specify \(\mathrm{SuNem}_q\), an additional normalization is imposed: |
||
| − | [[File:Sunem1map6.jpg|200px|thumb|$u\!+\!\mathrm i v=\mathrm{SuNem}_1(x\!+\!\mathrm i y)$]] |
||
| + | |||
| − | [[File:Sunem2map6.jpg|200px|thumb|$u\!+\!\mathrm i v=\mathrm{SuNem}_2(x\!+\!\mathrm i y)$]] |
||
| + | \[ |
||
| − | For the [[Nemtsov function]] |
||
| + | \mathrm{SuNem}_q(0) = 1. |
||
| − | $\mathrm{Nem}_q$, the [[superfunction]] $\mathrm{SuNem}_q~$ is real–holomorphic solution $F$ of the [[transfer equation]] |
||
| + | \] |
||
| + | |||
| + | The plot \(y=\mathrm{SuNem}_q(x)\) appears at left for several values of \(q\). |
||
| + | The function grows monotonically from \(0\) at \(-\infty\), reaches \(1\) at argument \(0\), and then increases rapidly for positive arguments. |
||
| + | Larger \(q\) produces faster growth. |
||
| + | |||
| + | Complex maps \(u+\mathrm i v=\mathrm{SuNem}_q(x+\mathrm i y)\) are displayed in figures at right for |
||
| + | \(q\!=\!0\) and \(q\!=\!2\). Regions with high density of contours (in vicinity of positive part of the real axis) are left empty; this is convenient mode to show [[complex map]]s of functions with fast growth. |
||
| + | |||
| + | To construct \(\mathrm{SuNem}_q\), one first constructs any superfunction \(F\) with the correct asymptotics, and then defines |
||
| + | \[ |
||
| − | $F(z\!+\!1)=\mathrm{Nem}_q\big( F(z)\big)$ |
||
| + | \mathrm{SuNem}_q(z) = F(x_1 + z), |
||
| + | \] |
||
| + | where \(x_1\) is the real number satisfying \(F(x_1)=1\). |
||
| − | with specific asymptotic behaviour at infinity, namely, |
||
| + | For [[transfer function]] \(\mathrm{nem}_q\), the |
||
| − | $\displaystyle |
||
| + | \(\mathrm{SuNem}_q\) seems to be the only real-holomorphic [[superfunction]] |
||
| − | F(z)=\frac{1}{\sqrt{-2 z}}\left( 1-\frac{q}{\sqrt{-2 z}} + O\big( \ln(-z)/z\big) \right)$ |
||
| + | that takes value unity at zero and approaches zero at \(x\pm \mathrm i \infty\); in this sense, \(\mathrm{SuNem}_q\) is the simplest [[superfunction]]. |
||
| + | == Abel function == |
||
| − | In order to specify function SuNem, the additional condition is assumed: |
||
| + | <div class="thumb tleft" style="float:left; width:200px; margin:-2px 18px 5px 0px; background-color:#fff; width:210px"> |
||
| − | $\mathrm{SuNem}_q(0)=1$ |
||
| + | {{pic|Aunemplot.jpg|200px}}<small><center>\(y=\mathrm{AuNem}_q(x)\) for \(q=0\), \(1\), \(2\)</center></small> |
||
| + | </div> |
||
| + | For the Abel function of the Nemtsov function, the notation [[AuNem]] is used. |
||
| − | (Similar condition is used to specify [[tetration]] as [[superfunction]] of exponent). |
||
| + | The explicit plot \(y=\mathrm{AuNem}_q(x)\) versus \(x\) is shown at left for \(q=0\), \(1\), and \(2\). |
||
| − | Explicit plot of function [[SuNem]] of the real argument is shown in figure at left, $y\!=\!\mathrm{SuNem}_q(x)$ is plotted versus $x$ for various values of $q$. |
||
| + | This plot coincides with reflecting the plots of \(\mathrm{SuNem}_q\) across the bisector of the first quadrant. |
||
| − | Function [[SuNem]] grows monotonously from zero at $-\infty$, takes value unity at zero and then grows quickly to infinity for positive values of the argument. |
||
| + | This symmetry provides a numerical test: |
||
| − | The larger is parameter $q$, the faster is the growth at $+\infty$. This behaviour corresponds to the intuitive expectations about this function. |
||
| + | \[ |
||
| − | Complex maps of function [[SuNem]] are shown in figures at right for $q\!=\!0$, $q\!=\!1$ and for $q\!=\!2$; |
||
| + | \mathrm{SuNem}_q(\mathrm{AuNem}_q(x)) = x, |
||
| + | \qquad |
||
| + | \mathrm{AuNem}_q = \mathrm{SuNem}_q^{-1}. |
||
| + | \] |
||
| + | As the inverse of the [[superfunction]], the [[Abel function]] satisfies the [[Abel equation]] |
||
| − | $u\!+\!\mathrm i v=\mathrm{SuNem}_q(x\!+\!\mathrm i y)$ |
||
| + | \[ |
||
| − | Maps for different values of $q$ look similar; however, the greater is $q$, the faster is the growth of $\mathrm{SuNem}_q$ along the real axis. This is seen also at the explicit plot in figure at left. |
||
| + | \mathrm{AuNem}_q(\mathrm{nem}_q(z)) = \mathrm{AuNem}_q(z) + 1. |
||
| + | \] |
||
| + | The normalization is |
||
| − | In order to construct function [[SuNem]], first, any superfunction $F$ with appropriate asymptotic behaviour is constructed; then, $\mathrm{SuNem}_q(z)=F(x_1+z)$ where $x_1$ is real solution of equation $F(x_1)=1$. |
||
| + | \[ |
||
| − | ==Abel function== |
||
| − | + | \mathrm{AuNem}_q(1) = 0, |
|
| + | \] |
||
| − | $q\!=\!0$, |
||
| − | $q\!=\!1$ and |
||
| − | $q\!=\!2$]] |
||
| − | For the [[Abel function]] of the [[Nemtsov function]], notation [[AuNem]] is suggested. |
||
| + | because \(\mathrm{SuNem}_q(0)=1\). |
||
| − | Explicit plot $y\!=\!\mathrm{AuNem}_q(x)$ versus $x$ is shown in figure at left for |
||
| − | $q\!=\!0$, |
||
| − | $q\!=\!1$ and |
||
| − | $q\!=\!2$. |
||
| − | The same plot can be obtained, reflecting the curves for [[SuNem]] from the bisektris of the First quadrant of the coordinate plane. This property can be used as a mumerical test of relation $\mathrm{SuNem}_q(\mathrm{АuNem}_q(x))=x$; it should be so, as |
||
| − | + | The asymptotic expansion of \(\mathrm{AuNem}_q\) near \(0\) follows from inverting the asymptotics of \(\mathrm{SuNem}_q\) at \(-\infty\).<br> |
|
| + | This expansion gives way to the efficient implementation, in analogy with the [[regular iteration]]. |
||
| + | == Iterates == |
||
| − | As inverse of the [[superfunction]], function [[AuNem]] satisfies the [[Abel equation]] |
||
| + | <div class="thumb tright" style="float:right; margin:-36px 0px 2px 8px; background-color:#fff"> |
||
| − | $\mathrm{AuNem}_q\big( \mathrm{Nem}_q(z)\big)=\mathrm{AuNem}_q(z)+1$ |
||
| + | {{pic|Itnem00plot.jpg|216px}}<small><center>\(y=\mathrm{nem}_0^{\,n}(x)\) for various \(n\)</center></small> |
||
| + | {{pic|Itnem10plot.jpg|216px}}<small><center>\(y=\mathrm{nem}_1^{\,n}(x)\) for various \(n\)</center></small> |
||
| + | {{pic|Itnem20plot.jpg|216px}}<small><center>\(y=\mathrm{nem}_2^{\,n}(x)\) for various \(n\)</center></small> |
||
| + | </div> |
||
| + | Using the functions \(\mathrm{SuNem}_q\) and \(\mathrm{AuNem}_q\), the \(n\)-th iterate of the Nemtsov function can be expressed as |
||
| − | Function AuNem satisfies also the additional condition |
||
| + | \[ |
||
| − | $\mathrm{AuNem}_q(1)=0$ |
||
| + | \mathrm{nem}_q^{\,n}(z) |
||
| + | = \mathrm{SuNem}_q\!\big(n + \mathrm{AuNem}_q(z)\big). |
||
| + | \] |
||
| + | Here, the number \(n\) of iterate has no need to be integer; the function can be iterated real or even complex number of times. |
||
| − | that is determined by the corresponding property of the SuNem, namely, that $\mathrm{SuNem}_q(0)\!=\!1~$. |
||
| + | Plots of the iterates for \(q=0\), \(q=1\), and \(q=2\) appear at right. |
||
| − | The asymptotic expansion of function [[AuNem]] at zero can be found, inverting the asymptotic expansion of function [[SuNem]] at $-\infty$; |
||
| + | For positive integer \(n\), the iterate grows rapidly; for negative \(n\), the growth is slow. |
||
| − | the coeffcieints of this expansion can be found also from the Abel equation. The expansion can be written as follows: |
||
| − | = |
+ | The zeroth iterate (\(n=0\)) is the identity function. |
| + | In the figures, this curve appears as a green line. |
||
| − | [[File:Itnem00plot.jpg|200px|thumb|$y\!=\!\mathrm{Nem}_0^{\,n}(x)$ versus $x$ at various $n$]] |
||
| − | [[File:Itnem10plot.jpg|200px|thumb|$y\!=\!\mathrm{Nem}_1^{\,n}(x)$ versus $x$ at various $n$]] |
||
| − | [[File:Itnem20plot.jpg|200px|thumb|$y\!=\!\mathrm{Nem}_2^{\,n}(x)$ versus $x$ at various $n$]] |
||
| + | Because \(\mathrm{ArqNem}_q\) has a singularity at \(0\), non-integer iterates are not defined at \(0\) or on the negative real axis, though they approach \(0\) from the right. |
||
| − | With functions [[SuNem]] and [[AuNem]], the $n$th [[iterate]] of the [[Nemtsov function]] can be expressed as follows |
||
| + | At least in some vicinity of the positive part of the real axis (moderate values of \(\Im(z)\)), |
||
| − | $\mathrm{Nem}_q^{\,n}(z)=\mathrm{AuNem}_q\big( n+\mathrm{AuNem}_q(z)\big)$ |
||
| + | the iterates satisfy the symmetry |
||
| + | \[ |
||
| + | \mathrm{nem}_q^{-n}(z) = \mathrm{ArqNem}_q^{\,n}(z). |
||
| + | \] |
||
| + | This relation holds until to reach the first branch cut of function [[AuNem]]\(_q\). |
||
| + | == Applications == |
||
| − | For |
||
| − | $q\!=\!0$, |
||
| − | $q\!=\!1$ and for |
||
| − | $q\!=\!2$, |
||
| − | these iterates are shown in figures at right. |
||
| − | These iterates look similar to other iterates of the fast growing functions. |
||
| + | The Nemtsov function was proposed as a candidate transfer function for which the superfunction and the Abel function would be difficult to construct using the [[exotic iterate]] at its fixed point \(0\). |
||
| − | At positive number $n$ of iterate, the iterate shows the fast growth; |
||
| + | The difficulty lay mostly in constructing the correct inverse function \(\mathrm{ArqNem}_q\), choosing branch cuts appropriately, and recognizing that \(\mathrm{ArqNem}_q\) rather than \(\mathrm{ArcNem}\) or \(\mathrm{ArkNem}\) should serve as the default inverse. |
||
| − | at negative values of $n$, the growth is slow. |
||
| + | Other inverse functions differ only in branch-cut placement and do not yield a real-holomorphic Abel function on as wide a domain. |
||
| − | The zeroth iterate ($n\!=\!0$), the iterates apperas as identity function. In the figures, the corresponding graphic is marked with green line. |
||
| + | Once the inverse iterates converge to the [[fixed point]], the [[exotic iteration]] becomes straightforward. |
||
| − | Due to the singularity of function [[ArqNem]] at zero, the non–integer iterates are not defined at zero and the negative part of the real axis, although they approach zero as the positive argument of the iterate becomes small. |
||
| + | The same approach can be used for other exotic [[transfer function]]s whose expansion at the fixed point begins with a linear term and a cubic term (the cubic coefficient can always be normalized to \(1\)). |
||
| + | The required transformation appears in the last row of the [[Table of superfunctions]]. |
||
| + | == Warning == |
||
| − | The curves of the iterates show the symmetry with respect to reflections from the bisectris of the First quadrant of the coordinate plane, as |
||
| + | The name “[[Nemtsov function]]’’ was chosen as a mnemonic connected to a notable event of the 21st century. |
||
| − | $\mathrm{Nem}_q^{-n}(z)=\mathrm{ArqNem}_q^{\,n}(z)$ |
||
| + | It is not intended as a political statement or as an attempt to appeal to the Russian usurper or his accomplices. |
||
| − | ==Applivation and the Discussion== |
||
| + | The ongoing rise of corruption <ref name="medvedko"/> indicates that moral appeals are meaningless in that context, even while some impostors pretend they can “[[end war in 24 hours]]’’ by [[appeasing aggression]] and [[war crime]]s. |
||
| − | The [[Nemtsov function]] is considered as a candidate of the [[transfer function]], for which the |
||
| − | [[superfunction]] and the [[Abel function]] are diffucult to construct with the [[exotic iterate]] at its [[fixed point]] zero. |
||
| + | Nevertheless, the editor reserves the right to use the most convenient system of notation. |
||
| − | Indeed, the construction required certain efforts, but they sere related mainly with construction of the inverse function [[ArqNem]], the efficient implementation and, especially, with guessing, that namely |
||
| − | [[ArqNem]] shouls be used to get the [[Abel function]] and non–integer iterates, that are holomorphic in the most of the complex plane. |
||
| + | == Acknowledgement == |
||
| − | For the [[Nemtsov function]], two other [[inverse function]]s have been constructed, they are denoted with hames |
||
| − | [[ArcNem]] and [[ArkNem]]. They have different positions of the cut lines, and, at the iterates, do not provide the |
||
| − | holomorphic Abel function. |
||
| + | [[ChatGPT]] helped to improve this article. |
||
| − | Once the iterates of the inverse function leads to the fixed point of the transfer function, the exotic iterates are straightforward. Other transfer functions can be considered in the similar way, assuming, that their expansion at the fixed point begins with the identity function and the cubic term. Without loss of generality, the coefficient at the cubic term can be treated as unity; the corresponding transform to this case is shown in the last row of the |
||
| − | [[Table of superfunctions]]. |
||
| − | ==References== |
+ | == References == |
| + | {{ref}} |
||
| − | <references/> |
||
| + | {{fer}} |
||
| − | http://mizugadro.mydns.jp/2016NEMTSOV/TRY00/23.pdf |
||
| − | Dmitrii Kouznetsov. Nemtsov function and its iterates. 2016, in preparation. |
||
| − | ==Keywords== |
+ | == Keywords == |
| − | [[Abel function]], |
+ | «[[Abel function]]», |
| − | [[ArqNem]], |
+ | «[[ArqNem]]», |
| − | [[AuNem]], |
+ | «[[AuNem]]», |
| − | [[Book]], |
+ | «[[Book]]», |
| − | [[C++]], |
+ | «[[C++]]», |
| − | [[Exotic iterate]], |
+ | «[[Exotic iterate]]», |
| + | «[[Exotic iteration]]», |
||
| − | [[Latex]], |
||
| − | [[ |
+ | «[[Latex]]», |
| + | «[[Mathematica]]», |
||
| − | [[Nemtsov function]], |
||
| + | «[[Nemtsov function]]», |
||
| − | [[Putin killed Nemtsov]], |
||
| + | «[[Putin killed Nemtsov]]», |
||
| − | [[SuNem]], |
||
| − | [[ |
+ | «[[SuNem]]», |
| − | [[ |
+ | «[[Superfunction]]», |
| + | «[[Superfunctions]]», |
||
| − | [[Table of superfunctions]] |
||
| + | «[[Table of superfunctions]]», |
||
| + | «[[Немцов Борис Ефимович]]», |
||
| + | «[[Путин убил Немцова]]», |
||
[[Category:Abel function]] |
[[Category:Abel function]] |
||
| + | [[Category:Abelfunction]] |
||
[[Category:ArqNem]] |
[[Category:ArqNem]] |
||
[[Category:AuNem]] |
[[Category:AuNem]] |
||
Latest revision as of 13:27, 7 December 2025
The Nemtsov function is a special kind of polynomial, suggested as an example of a transfer function in the book «Superfunctions» [1]. The description is also available as the Mizugadro Preprint [2].
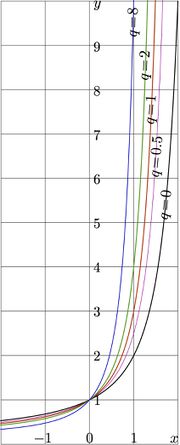
The Nemtsov function \(y=\mathrm{nem}_q(x)= x+x^3+q\,x^4\) is shown in the figure at right for various \(q\ge 0\).
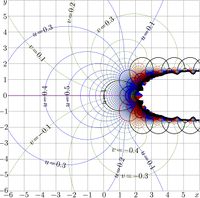
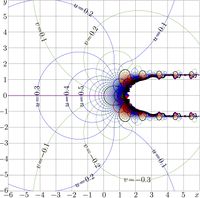
Complex maps of \(\mathrm{nem}_q\) are shown in the left column of the figure below. The right column shows similar maps for the inverse function \(\mathrm{ArqNem}_q=\mathrm{nem}_q^{-1}\).
This article describes the Nemtsov function and its related functions: the inverse function ArqNem, the superfunction SuNem, and the Abel function AuNem.
Motivation
The Nemtsov function serves as an example of a real-holomorphic transfer function with a real fixed point, where the usual regular iteration method for constructing a superfunction cannot be applied directly. The editor did not find any simpler example of this type other than this specific fourth-order polynomial.
The function was introduced as an attempt to construct an “exotic’’ transfer function for which a growing real-holomorphic superfunction could not be produced by the usual methods appearing in the «Table of superfunctions». This attempt failed — the superfunction for the Nemtsov function *can* be constructed, and is described below.
The expansion of the Nemtsov function at its fixed point begins with a linear term whose coefficient is unity. This prevents the use of standard regular iteration [3], which works for the exponential to base \(\sqrt{2}\).
The situation is similar to the exponential to base \(\exp(1/\mathrm e)\) [4], but the Nemtsov function lacks the quadratic term, so the exotic iteration of [4] cannot be used as is.
A closer analogy is the case of the sine function [5], but sine is antisymmetric, \(\sin(-z)=-\sin(z)\), which simplifies its analysis. The Nemtsov function for \(q>0\) has no such symmetry, leading initially to doubts whether a superfunction could be constructed.
Eventually, the construction succeeded.
The need for a special name for this function emerged on 2015-02-27, the day when Putin killed Nemtsov. As of 2025, no other scientific concept attached to that event has appeared. The total corruption in Russia [7] prevents professional investigation of the crime. Thus, the family name “Nemtsov’’ serves as a historical timestamp.
By 2025, no better notation for this polynomial has been proposed. The function symbol is written as lowercase \(\mathrm{nem}\), following the convention for mathematical functions, even though “Nemtsov’’ is a proper name. Capitalization is used only when distinguishing it from derived functions such as ArqNem, AuNem, and SuNem.
Definition and notations
Let \(q\ge 0\) be a real parameter. The Nemtsov function is defined for complex argument \(z\) by
\[ \mathrm{nem}_q(z)=z+z^3+q\,z^4 \tag{1} \]
For \(q>0\), the algorithms described in the first Russian edition of «Суперфункции» (2014) [8] cannot be applied in their original form; a small generalization is required. Thus the function \(\mathrm{nem}_q\) is treated as a transfer function.
This appears to be the last remaining attempt (as of 2025) to produce a real-holomorphic, growing transfer function whose superfunction cannot be constructed by methods already known in the literature.
But again, the attempt fails: both the superfunction SuNem and the Abel function AuNem are constructed using a method similar to that used for the sine function.
Associated functions:
Inverse function: \(\mathrm{ArqNem}_q\), satisfying \[ \mathrm{nem}_q(\mathrm{ArqNem}_q(z)) = z \]
Superfunction \(\mathrm{SuNem}_q\), satisfying \[ \mathrm{SuNem}_q(z+1) = \mathrm{nem}_q(\mathrm{SuNem}_q(z)) \]
Abel function: \(\mathrm{AuNem}_q=\mathrm{SuNem}_q^{-1}\), satisfying
\[ \mathrm{AuNem}_q(\mathrm{nem}_q(z)) = \mathrm{AuNem}_q(z) + 1 \]
Several inverse functions exist: ArcNem, ArkNem, and ArqNem. They differ in branch-cut placement. ArqNem turns out to be the correct one for defining holomorphic non-integer iterates near the positive real axis; therefore it is adopted as the default inverse.
Inverse function
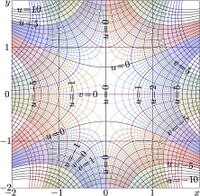
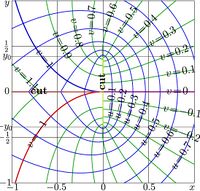
To construct the inverse function in the complex plane, one must locate the saddle points and choose suitable branch cuts. In the complex maps shown previously, the yellow lines indicate the branch cuts for functions \(\mathrm{ArqNem}_0\) and \(\mathrm{ArqNem}_2\). These lines connect the two complex branch points of \(\mathrm{ArqNem}_q\).
For real \(q\), the Nemtsov function is real-holomorphic in the whole complex plane:
\[ \mathrm{nem}_q(z^{*}) = \mathrm{nem}_q(z)^{*}. \]
For positive real arguments, the function grows monotonically. This monotonicity is inherited by its inverse \(\mathrm{ArqNem}_q\), its Abel function \(\mathrm{AuNem}_q\), and its real iterates.
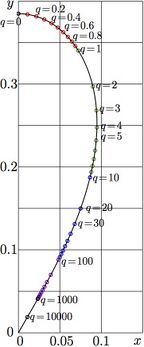
The inverse function \(\mathrm{ArqNem}_q\) has complex branch points. One of them is described explicitly by the function NemBran. At \(z=\mathrm{NemBran}(q)\), the derivative of \(\mathrm{ArqNem}_q(z)\) becomes infinite.
The branch points arise from the complex solutions \(A\) of the equation
\[ \mathrm{nem}_q'(A) = 0. \]
One such solution is denoted \(\mathrm{NemBra}(q)\), and its image
\[ \mathrm{NemBran}(q) = \mathrm{nem}_q(\mathrm{NemBra}(q)). \]
For positive \(q\), both real and imaginary parts of \(\mathrm{NemBra}(q)\) and \(\mathrm{NemBran}(q)\) are small (well below unity).
Once \(\mathrm{NemBra}\) is implemented, an efficient algorithm for inverse functions becomes possible. Three versions—ArcNem, ArkNem, and ArqNem—differ only in branch-cut structure. ArqNem is best suited for constructing holomorphic non-integer iterates near the positive real axis.
The C++ implementation of \(\mathrm{ArqNem}_q\) is available as arqnem.cin. Parameter \(q\) is stored in the global variable `Q`. Before evaluating \(\mathrm{ArqNem}_q(z)\), the corresponding branch point must be computed via nembran.cin and stored in global variables (real and imaginary parts).
Superfunction
For the transfer function \(\mathrm{nem}_q\), the superfunction \(\mathrm{SuNem}_q\) is the real-holomorphic solution \(F\) of the transfer equation
\[ F(z+1) = \mathrm{nem}_q(F(z)), \]
with the asymptotic condition at \(-\infty\):
\[ F(z) = \frac{1}{\sqrt{-2z}} \left( 1 - \frac{q}{\sqrt{-2z}} + O\!\left( \frac{\ln(-z)}{z} \right) \right), \qquad z\to -\infty. \]
To fully specify \(\mathrm{SuNem}_q\), an additional normalization is imposed:
\[ \mathrm{SuNem}_q(0) = 1. \]
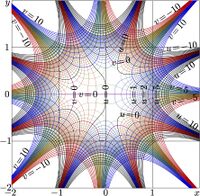
The plot \(y=\mathrm{SuNem}_q(x)\) appears at left for several values of \(q\). The function grows monotonically from \(0\) at \(-\infty\), reaches \(1\) at argument \(0\), and then increases rapidly for positive arguments. Larger \(q\) produces faster growth.
Complex maps \(u+\mathrm i v=\mathrm{SuNem}_q(x+\mathrm i y)\) are displayed in figures at right for \(q\!=\!0\) and \(q\!=\!2\). Regions with high density of contours (in vicinity of positive part of the real axis) are left empty; this is convenient mode to show complex maps of functions with fast growth.
To construct \(\mathrm{SuNem}_q\), one first constructs any superfunction \(F\) with the correct asymptotics, and then defines
\[ \mathrm{SuNem}_q(z) = F(x_1 + z), \]
where \(x_1\) is the real number satisfying \(F(x_1)=1\).
For transfer function \(\mathrm{nem}_q\), the \(\mathrm{SuNem}_q\) seems to be the only real-holomorphic superfunction that takes value unity at zero and approaches zero at \(x\pm \mathrm i \infty\); in this sense, \(\mathrm{SuNem}_q\) is the simplest superfunction.
Abel function
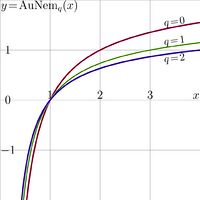
For the Abel function of the Nemtsov function, the notation AuNem is used.
The explicit plot \(y=\mathrm{AuNem}_q(x)\) versus \(x\) is shown at left for \(q=0\), \(1\), and \(2\). This plot coincides with reflecting the plots of \(\mathrm{SuNem}_q\) across the bisector of the first quadrant. This symmetry provides a numerical test:
\[ \mathrm{SuNem}_q(\mathrm{AuNem}_q(x)) = x, \qquad \mathrm{AuNem}_q = \mathrm{SuNem}_q^{-1}. \]
As the inverse of the superfunction, the Abel function satisfies the Abel equation
\[ \mathrm{AuNem}_q(\mathrm{nem}_q(z)) = \mathrm{AuNem}_q(z) + 1. \]
The normalization is
\[ \mathrm{AuNem}_q(1) = 0, \]
because \(\mathrm{SuNem}_q(0)=1\).
The asymptotic expansion of \(\mathrm{AuNem}_q\) near \(0\) follows from inverting the asymptotics of \(\mathrm{SuNem}_q\) at \(-\infty\).
This expansion gives way to the efficient implementation, in analogy with the regular iteration.
Iterates



Using the functions \(\mathrm{SuNem}_q\) and \(\mathrm{AuNem}_q\), the \(n\)-th iterate of the Nemtsov function can be expressed as
\[ \mathrm{nem}_q^{\,n}(z) = \mathrm{SuNem}_q\!\big(n + \mathrm{AuNem}_q(z)\big). \]
Here, the number \(n\) of iterate has no need to be integer; the function can be iterated real or even complex number of times.
Plots of the iterates for \(q=0\), \(q=1\), and \(q=2\) appear at right. For positive integer \(n\), the iterate grows rapidly; for negative \(n\), the growth is slow.
The zeroth iterate (\(n=0\)) is the identity function. In the figures, this curve appears as a green line.
Because \(\mathrm{ArqNem}_q\) has a singularity at \(0\), non-integer iterates are not defined at \(0\) or on the negative real axis, though they approach \(0\) from the right.
At least in some vicinity of the positive part of the real axis (moderate values of \(\Im(z)\)), the iterates satisfy the symmetry \[ \mathrm{nem}_q^{-n}(z) = \mathrm{ArqNem}_q^{\,n}(z). \] This relation holds until to reach the first branch cut of function AuNem\(_q\).
Applications
The Nemtsov function was proposed as a candidate transfer function for which the superfunction and the Abel function would be difficult to construct using the exotic iterate at its fixed point \(0\). The difficulty lay mostly in constructing the correct inverse function \(\mathrm{ArqNem}_q\), choosing branch cuts appropriately, and recognizing that \(\mathrm{ArqNem}_q\) rather than \(\mathrm{ArcNem}\) or \(\mathrm{ArkNem}\) should serve as the default inverse.
Other inverse functions differ only in branch-cut placement and do not yield a real-holomorphic Abel function on as wide a domain.
Once the inverse iterates converge to the fixed point, the exotic iteration becomes straightforward. The same approach can be used for other exotic transfer functions whose expansion at the fixed point begins with a linear term and a cubic term (the cubic coefficient can always be normalized to \(1\)). The required transformation appears in the last row of the Table of superfunctions.
Warning
The name “Nemtsov function’’ was chosen as a mnemonic connected to a notable event of the 21st century.
It is not intended as a political statement or as an attempt to appeal to the Russian usurper or his accomplices. The ongoing rise of corruption [7] indicates that moral appeals are meaningless in that context, even while some impostors pretend they can “end war in 24 hours’’ by appeasing aggression and war crimes.
Nevertheless, the editor reserves the right to use the most convenient system of notation.
Acknowledgement
ChatGPT helped to improve this article.
References
- ↑
https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862
https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3
https://mizugadro.mydns.jp/BOOK/468.pdf
Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020. - ↑
https://mizugadro.mydns.jp/PAPERS/2016nemtsov.pdf
Dmitrii Kouznetsov. Nemtsov function and its iterates. Mizugadro Preprint, 2016. - ↑
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
https://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf
D. Kouznetsov, H. Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727–1756. - ↑ 4.0 4.1
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf
https://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf
H. Trappmann, D. Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation, 81 (2012), 2207–2227. - ↑
http://www.pphmj.com/references/8246.htm
https://mizugadro.mydns.jp/PAPERS/2014susin.pdf
Dmitrii Kouznetsov. SUPER SIN. Far East Journal of Mathematical Sciences 85(2), 219–238 (2014). - ↑ http://nemtsov.ru Борис Немцов
- ↑ 7.0 7.1
http://kremlin.ru/transcripts/1566
D. Medvedev: Corruption in our country has acquired not just a large-scale character; it has become a habitual, everyday phenomenon... (2008) - ↑ http://mizugadro.mydns.jp/BOOK/202.pdf Дмитрий Кузнецов. Суперфункции. Lambett Academic Publishing, 2014. (in Russian)
Keywords
«Abel function», «ArqNem», «AuNem», «Book», «C++», «Exotic iterate», «Exotic iteration», «Latex», «Mathematica», «Nemtsov function», «Putin killed Nemtsov», «SuNem», «Superfunction», «Superfunctions», «Table of superfunctions»,