Difference between revisions of "File:SuZexD1mapT.png"

From TORI
Jump to navigation Jump to search
(Importing image file)
 
Line 1: Line 1:
  +
[[Complex map]] of function [[SuZex]], which is entire [[superfunction]] of [[Zex]], $\mathrm{zex}(z)=z\exp(z)$.
−
Importing image file
  
  +
  +
$u\!+\!\mathrm i v = \mathrm{SuZex}(c\!+\!\mathrm i y)$
  +
  +
[[SuZex]] is built-up at the fixed point zero from asymptotic behavior; the approximation below is implemented:
  +
:$\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \displaystyle
  +
f(z)= \frac{-1}{z} +\frac{ \ln(-z)}{2 z^2}+ \frac{-.05\ln(-z)^2-.02\ln(-z)-.4}{z^3}$
  +
For integer $n$,
  +
:$\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \displaystyle
  +
F_n(z)=\mathrm{zex}^n\Big( z\!-\!n) \Big)$
  +
The constant $x_n$ is chosen as solution of equation $F_n(x_n)\!=\!1$. Then, the superfunction is evaluated as iteration
  +
:$\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \displaystyle
  +
\mathrm{SuZex}(z)=F_n(x_n\!+\!z)$
  +
for integer $n$.
  +
  +
The generator below uses value $n\!=\!16$, which is sufficient to get the camera-ready copy. For the precise computation, more terms in the expansion (1) should be calculated.
  +
The precise implementation (with 14 decimal digits) is loaded as [[SuZex.cin]].
  +
  +
==[[C++]] generator of curves==
  +
#include <math.h>
  +
#include <stdio.h>
  +
#include <stdlib.h>
  +
#define DB double
  +
#define DO(x,y) for(x=0;x<y;x++)
  +
using namespace std;
  +
#include<complex>
  +
typedef complex<double> z_type;
  +
#define Re(x) x.real()
  +
#define Im(x) x.imag()
  +
#define I z_type(0.,1.)
  +
#include "conto.cin"
  +
// #include "fsexp.cin"
  +
//#include "fslog.cin"
  +
  +
z_type zex(z_type z){ return z*exp(z);}
  +
  +
int Nitera=16;
  +
  +
z_type suzex0b(z_type z){ return -1./z; }
  +
// z_type suzex0(z_type z){ z_type L=log(-z); return (-1.+.5*L/z)/z; }
  +
z_type suzex0(z_type z){ z_type L=log(-z); return (-1.+(.5*L + (-.05*L*L-.02*L-.4)/z)/z)/z; }
  +
  +
z_type suzexn(int n, z_type z){int m; z-=0.+n; z=suzex0(z); DO(m,n) z=zex(z); return z; }
  +
  +
main(){ int j,k,m,n; DB x1,x,y, p,q, t; z_type z,c,d, cu,cd;
  +
x1=-1.04;
  +
DO(n,18){ y=Re(suzexn(Nitera,x1)); x=y-1.; x1-=1.5*x; printf("%18.16f %18.16f\n", x1,y);}
  +
getchar();
  +
  +
int M=601,M1=M+1;
  +
int N=401,N1=N+1;
  +
DB X[M1],Y[N1];
  +
DB *g, *f, *w; // w is working array.
  +
g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
  +
f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
  +
w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
  +
char v[M1*N1]; // v is working array
  +
FILE *o;o=fopen("suZexMap.eps","w"); ado(o,1202,1202);
  +
fprintf(o,"601 601 translate\n 100 100 scale\n");
  +
fprintf(o,"1 setlinejoin 2 setlinecap\n");
  +
DO(m,M1) X[m]=-6.+.02*(m-.1);
  +
//DO(n,N1) Y[n]=-5.+.02*(n-.5);
  +
for(n=0;n<N1;n++) { Y[n]=0.6*sinh((3./200.)*(n-200.5)); printf("%3d %9.6f\n",n,Y[n]); }
  +
for(m=-6;m<7;m++) {M(m,-6)L(m,6)}
  +
for(n=-6;n<7;n++) {M( -6,n)L(6,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
  +
DO(m,M1)DO(n,N1){ g[m*N1+n]=999;
  +
f[m*N1+n]=999;}
  +
DO(m,M1){x=X[m]; if(m/10*10==m) printf("x=%6.3f\n",x);
  +
DO(n,N1){y=Y[n]; z=z_type(x,y); //if(abs(z+2.)>.019)
  +
{
  +
c=suzexn(Nitera,z+x1);
  +
p=Re(c); q=Im(c);
  +
if(p>-19 && p<19 && fabs(q)>1.e-12 && fabs(p)>1.e-12) g[m*N1+n]=p;
  +
if(p>-19 && p<19 && fabs(q)>1.e-12 && fabs(p)>1.e-12) f[m*N1+n]=q;
  +
}
  +
}}
  +
fprintf(o,"1 setlinejoin 1 setlinecap\n");
  +
p=2.;q=.3;
  +
  +
for(m=-8;m<8;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);fprintf(o,".007 W 0 .6 0 RGB S\n");
  +
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);fprintf(o,".007 W .9 0 0 RGB S\n");
  +
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);fprintf(o,".007 W 0 0 .9 RGB S\n");
  +
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".02 W .8 0 0 RGB S\n");
  +
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".02 W 0 0 .8 RGB S\n");
  +
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".02 W .5 0 .5 RGB S\n");
  +
for(m=-16;m<17;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
  +
  +
//#include "plofu.cin"
  +
fprintf(o,"0 setlinejoin 0 setlinecap\n");
  +
fprintf(o,"showpage\n");
  +
fprintf(o,"%c%cTrailer\n",'%','%');
  +
fclose(o); free(f); free(g); free(w);
  +
system("epstopdf SuZexMap.eps");
  +
system( "open SuZexMap.pdf"); //for macintosh
  +
getchar(); system("killall Preview"); // For macintosh
  +
}
  +
  +
  +
==[[Latex]] generator of labels==
  +
  +
% <nowiki> %<br>
  +
\documentclass[12pt]{article} % <br>
  +
\paperheight 1228px % <br>
  +
\paperwidth 1236px % <br>
  +
\textwidth 1394px % <br>
  +
\textheight 1300px % <br>
  +
\topmargin -104px % <br>
  +
\oddsidemargin -78px % <br>
  +
\usepackage{graphics} % <br>
  +
\usepackage{rotating} % <br>
  +
\newcommand \sx {\scalebox} % <br>
  +
\newcommand \rot {\begin{rotate}} % <br>
  +
\newcommand \ero {\end{rotate}} % <br>
  +
\newcommand \ing {\includegraphics} % <br>
  +
\newcommand \rmi {\mathrm{i}} % <br>
  +
\begin{document} % <br>
  +
\newcommand \zoomax { % <br>
  +
\put(18,1206){\sx{3.3}{$y$}} % <br>
  +
\put(18,1113){\sx{3}{$5$}} % <br>
  +
\put(18,1013){\sx{3}{$4$}} % <br>
  +
\put(18, 913){\sx{3}{$3$}} % <br>
  +
\put(18, 813){\sx{3}{$2$}} % <br>
  +
\put(18, 713){\sx{3}{$1$}} % <br>
  +
\put(18, 613){\sx{3}{$0$}} % <br>
  +
\put(-6, 513){\sx{3}{$-1$}} % <br>
  +
\put(-6, 413){\sx{3}{$-2$}} % <br>
  +
\put(-6, 313){\sx{3}{$-3$}} % <br>
  +
\put(-6, 213){\sx{3}{$-4$}} % <br>
  +
\put(-6, 113){\sx{3}{$-5$}} % <br>
  +
\put(-6, 013){\sx{3}{$-6$}} % <br>
  +
\put(014, -5){\sx{3}{$-6$}} % <br>
  +
\put(114, -5){\sx{3}{$-5$}} % <br>
  +
\put(214, -5){\sx{3}{$-4$}} % <br>
  +
\put(314, -5){\sx{3}{$-3$}} % <br>
  +
\put(414, -5){\sx{3}{$-2$}} % <br>
  +
\put(514, -5){\sx{3}{$-1$}} % <br>
  +
\put(635, -5){\sx{3}{$0$}} % <br>
  +
\put(735, -5){\sx{3}{$1$}} % <br>
  +
\put(835, -5){\sx{3}{$2$}} % <br>
  +
\put(935, -5){\sx{3}{$3$}} % <br>
  +
\put(1035, -5){\sx{3}{$4$}} % <br>
  +
\put(1135, -5){\sx{3}{$5$}} % <br>
  +
\put(1227,-4){\sx{3}{$x$}} % <br>
  +
} % <br>
  +
\parindent 0pt % <br>
  +
\sx{1}{\begin{picture}(1252,1220) % <br>
  +
%\put(40,20){\ing{b271tMap3}} % <br>
  +
%\put(40,20){\ing{ExpMap}} % <br>
  +
\put(40,20){\ing{SuZexMap}} % <br>
  +
\zoomax % <br>
  +
\put(290,611){\sx{4}{$v\!=\!0$}} % <br>
  +
\put(183,560){\sx{4}{\rot{90}$u\!=\!0.2$\ero}} % <br>
  +
\put(468,560){\sx{4}{\rot{90}$u\!=\!0.4$\ero}} % <br>
  +
\put(696,118){\sx{4}{\rot{83}$u\!=\!0$\ero}} %<br>
  +
\put(980,236){\sx{4}{\rot{24}$u\!=\!-0.2$\ero}} %<br>
  +
\put(790, 44){\sx{4}{\rot{38}$v\!=\!-0.2$\ero}} %<br>
  +
\end{picture}} % <br>
  +
\end{document} % <br>
  +
</nowiki>
  +
  +
[[Category:SuZex]]
  +
[[Category:Zex]]
  +
[[Category:Superfunction]]
  +
[[Category:Regular iteration]]

Revision as of 09:43, 21 June 2013

Complex map of function SuZex, which is entire superfunction of Zex, $\mathrm{zex}(z)=z\exp(z)$.

$u\!+\!\mathrm i v = \mathrm{SuZex}(c\!+\!\mathrm i y)$

SuZex is built-up at the fixed point zero from asymptotic behavior; the approximation below is implemented:

$\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \displaystyle

f(z)= \frac{-1}{z} +\frac{ \ln(-z)}{2 z^2}+ \frac{-.05\ln(-z)^2-.02\ln(-z)-.4}{z^3}$ For integer $n$,

$\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \displaystyle

F_n(z)=\mathrm{zex}^n\Big( z\!-\!n) \Big)$ The constant $x_n$ is chosen as solution of equation $F_n(x_n)\!=\!1$. Then, the superfunction is evaluated as iteration

$\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \displaystyle

\mathrm{SuZex}(z)=F_n(x_n\!+\!z)$ for integer $n$.

The generator below uses value $n\!=\!16$, which is sufficient to get the camera-ready copy. For the precise computation, more terms in the expansion (1) should be calculated. The precise implementation (with 14 decimal digits) is loaded as SuZex.cin.

C++ generator of curves

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include<complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
// #include "fsexp.cin"
//#include "fslog.cin"

z_type zex(z_type z){ return z*exp(z);} 

int Nitera=16;

z_type suzex0b(z_type z){ return -1./z; }

// z_type suzex0(z_type z){ z_type L=log(-z); return (-1.+.5*L/z)/z; } 

z_type suzex0(z_type z){ z_type L=log(-z); return (-1.+(.5*L + (-.05*L*L-.02*L-.4)/z)/z)/z; }

z_type suzexn(int n, z_type z){int m;  z-=0.+n; z=suzex0(z); DO(m,n) z=zex(z); return z; } 

main(){ int j,k,m,n; DB x1,x,y, p,q, t; z_type z,c,d, cu,cd;
x1=-1.04;
DO(n,18){ y=Re(suzexn(Nitera,x1)); x=y-1.; x1-=1.5*x; printf("%18.16f %18.16f\n", x1,y);}
getchar();

int M=601,M1=M+1;
int N=401,N1=N+1;
DB X[M1],Y[N1];
DB *g, *f, *w; // w is working array.
g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
char v[M1*N1]; // v is working array
FILE *o;o=fopen("suZexMap.eps","w");  ado(o,1202,1202);
fprintf(o,"601 601 translate\n 100 100 scale\n");
fprintf(o,"1 setlinejoin 2 setlinecap\n");
DO(m,M1) X[m]=-6.+.02*(m-.1);
//DO(n,N1) Y[n]=-5.+.02*(n-.5); 
for(n=0;n<N1;n++) { Y[n]=0.6*sinh((3./200.)*(n-200.5)); printf("%3d %9.6f\n",n,Y[n]); }
for(m=-6;m<7;m++) {M(m,-6)L(m,6)}
for(n=-6;n<7;n++) {M(  -6,n)L(6,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){      g[m*N1+n]=999;
                       f[m*N1+n]=999;}
DO(m,M1){x=X[m]; if(m/10*10==m) printf("x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); //if(abs(z+2.)>.019)
      { 
c=suzexn(Nitera,z+x1);
        p=Re(c); q=Im(c);
        if(p>-19 && p<19 &&  fabs(q)>1.e-12 && fabs(p)>1.e-12) g[m*N1+n]=p;
        if(p>-19 && p<19 &&  fabs(q)>1.e-12 && fabs(p)>1.e-12) f[m*N1+n]=q;
      }
       }}
fprintf(o,"1 setlinejoin 1 setlinecap\n");
p=2.;q=.3;

for(m=-8;m<8;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);fprintf(o,".007 W 0 .6 0 RGB S\n");
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);fprintf(o,".007 W .9 0 0 RGB S\n");
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);fprintf(o,".007 W 0 0 .9 RGB S\n");
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".02 W .8 0 0 RGB S\n");
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".02 W 0 0 .8 RGB S\n");
               conto(o,f,w,v,X,Y,M,N, (0.  ),-p,p); fprintf(o,".02 W .5 0 .5 RGB S\n");
for(m=-16;m<17;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");

//#include "plofu.cin"
fprintf(o,"0 setlinejoin 0 setlinecap\n");
fprintf(o,"showpage\n");
fprintf(o,"%c%cTrailer\n",'%','%');
fclose(o);  free(f); free(g); free(w);
      system("epstopdf SuZexMap.eps"); 
      system(    "open SuZexMap.pdf"); //for macintosh
      getchar(); system("killall Preview"); // For macintosh
}


Latex generator of labels

% %<br> \documentclass[12pt]{article} % <br> \paperheight 1228px % <br> \paperwidth 1236px % <br> \textwidth 1394px % <br> \textheight 1300px % <br> \topmargin -104px % <br> \oddsidemargin -78px % <br> \usepackage{graphics} % <br> \usepackage{rotating} % <br> \newcommand \sx {\scalebox} % <br> \newcommand \rot {\begin{rotate}} % <br> \newcommand \ero {\end{rotate}} % <br> \newcommand \ing {\includegraphics} % <br> \newcommand \rmi {\mathrm{i}} % <br> \begin{document} % <br> \newcommand \zoomax { % <br> \put(18,1206){\sx{3.3}{$y$}} % <br> \put(18,1113){\sx{3}{$5$}} % <br> \put(18,1013){\sx{3}{$4$}} % <br> \put(18, 913){\sx{3}{$3$}} % <br> \put(18, 813){\sx{3}{$2$}} % <br> \put(18, 713){\sx{3}{$1$}} % <br> \put(18, 613){\sx{3}{$0$}} % <br> \put(-6, 513){\sx{3}{$-1$}} % <br> \put(-6, 413){\sx{3}{$-2$}} % <br> \put(-6, 313){\sx{3}{$-3$}} % <br> \put(-6, 213){\sx{3}{$-4$}} % <br> \put(-6, 113){\sx{3}{$-5$}} % <br> \put(-6, 013){\sx{3}{$-6$}} % <br> \put(014, -5){\sx{3}{$-6$}} % <br> \put(114, -5){\sx{3}{$-5$}} % <br> \put(214, -5){\sx{3}{$-4$}} % <br> \put(314, -5){\sx{3}{$-3$}} % <br> \put(414, -5){\sx{3}{$-2$}} % <br> \put(514, -5){\sx{3}{$-1$}} % <br> \put(635, -5){\sx{3}{$0$}} % <br> \put(735, -5){\sx{3}{$1$}} % <br> \put(835, -5){\sx{3}{$2$}} % <br> \put(935, -5){\sx{3}{$3$}} % <br> \put(1035, -5){\sx{3}{$4$}} % <br> \put(1135, -5){\sx{3}{$5$}} % <br> \put(1227,-4){\sx{3}{$x$}} % <br> } % <br> \parindent 0pt % <br> \sx{1}{\begin{picture}(1252,1220) % <br> %\put(40,20){\ing{b271tMap3}} % <br> %\put(40,20){\ing{ExpMap}} % <br> \put(40,20){\ing{SuZexMap}} % <br> \zoomax % <br> \put(290,611){\sx{4}{$v\!=\!0$}} % <br> \put(183,560){\sx{4}{\rot{90}$u\!=\!0.2$\ero}} % <br> \put(468,560){\sx{4}{\rot{90}$u\!=\!0.4$\ero}} % <br> \put(696,118){\sx{4}{\rot{83}$u\!=\!0$\ero}} %<br> \put(980,236){\sx{4}{\rot{24}$u\!=\!-0.2$\ero}} %<br> \put(790, 44){\sx{4}{\rot{38}$v\!=\!-0.2$\ero}} %<br> \end{picture}} % <br> \end{document} % <br>

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current17:50, 20 June 2013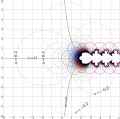Thumbnail for version as of 17:50, 20 June 20132,576 × 2,559 (1.04 MB)Maintenance script (talk | contribs)Importing image file

You cannot overwrite this file.

The following page uses this file:

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=File:SuZexD1mapT.png&oldid=5243"