Difference between revisions of "Maps of tetration"
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{top}} |
||
| ⚫ | |||
| + | <div style="float:right; margin:-72px 0px 4px 8px; background-color:#fff; font-size:12px; width:400px;"> |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| + | |||
| ⚫ | |||
| + | |||
| ⚫ | |||
| + | |||
| ⚫ | |||
| + | |||
| ⚫ | |||
| + | </center> |
||
| + | </div> |
||
| ⚫ | |||
| + | |||
| ⚫ | |||
| + | |||
| + | Below, the [[complex map]]s are shown. |
||
| ⚫ | |||
<poem> |
<poem> |
||
| − | + | \(b=\sqrt{2} \approx 1.41\) |
|
| − | + | \(b=\exp(1/\mathrm e) \approx 1.44\) |
|
| − | + | \(b=1.5\) |
|
| − | + | \(b=2\) |
|
| − | + | \(b=\mathrm e \approx 2.71\) |
|
| − | + | \(b=1.52598338517+0.0178411853321 \,\mathrm i\) |
|
</poem> |
</poem> |
||
| − | Tetration is shown with lines of constant real part |
+ | [[Tetration]] tet is shown with lines of constant real part \(u\) and lines of constant imaginary part \(v\); |
| − | + | \(u\!+\!\mathrm i v=\mathrm {tet}_b(x\!+\!\mathrm i y)\) |
|
| − | == |
+ | == <i>b</i>=sqrt(2)== |
| − | For this case, the regular iteration at [[fixed point]] |
+ | For this case, the [[regular iteration]] at [[fixed point]] \(L=2\) is used. |
The evaluation is described in the [[Mathematics of Computation]] |
The evaluation is described in the [[Mathematics of Computation]] |
||
<ref> |
<ref> |
||
| − | + | https://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html <br> |
|
| − | + | https://mizugadro.mydns.jp/PAPERS/2010q2.pdf |
|
| − | D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. |
+ | D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). [[Mathematics of Computation]], 2010, v.79, p.1727-1756. |
</ref>. |
</ref>. |
||
| − | == |
+ | ==<i>b</i>= e^(1/e) (approximately 1.44)== |
| − | For |
+ | For \(b=\exp(1/\mathrm e)\approx 1.44\), the [[exotic iteration]] at [[fixed point]] \(L=\mathrm e\approx 2.71\) is used. |
| − | The evaluation is described |
+ | The evaluation is described at the [[Mathematics of Computation]] |
<ref> |
<ref> |
||
| − | + | https://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf <br> |
|
| − | + | https://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf <br> |
|
| − | + | https://mizugadro.mydns.jp/PAPERS/2011e1e.pdf |
|
| − | H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation |
+ | H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). [[Mathematics of Computation]], 2012, v.81, p.2207-2227. ISSN 1088-6842(e) ISSN 0025-5718(p) |
| − | </ref>. |
+ | </ref>, 2012. |
| − | == |
+ | ==<i>b</i> > e^(1/e) == |
| − | For |
+ | For \(b>\exp(1/\mathrm e)\approx 1.44\), the |
[[Cauchi integral]] is used for evaluation. It is described in [[Mathematics of Computation]] |
[[Cauchi integral]] is used for evaluation. It is described in [[Mathematics of Computation]] |
||
<ref name=analuxp> |
<ref name=analuxp> |
||
| − | + | https://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html <br> |
|
| − | + | https://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf |
|
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
</ref>. |
</ref>. |
||
| − | Historically, evaluation for the case |
+ | Historically, evaluation for the case \(b=\mathrm e\) was first to be reported. |
| − | Namely for this case, the special |
+ | Namely for this case, the special code [[fsexp.cin]] is loaded; it is described in [[Vladikavkaz Mathematical Jorunal]] |
<ref name=vladie> |
<ref name=vladie> |
||
| − | + | https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf |
|
| − | D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. |
+ | D.Kouznetsov. Superexponential as special function. [[Vladikavkaz Mathematical Journal]], 2010, v.12, issue 2, p.31-45. |
</ref>. |
</ref>. |
||
| + | The same algorithm can be used also for other values of base; in particular, for \(b=1.5\) and for \(b=2\); |
||
| ⚫ | |||
| + | these cases are shown in figures at right. |
||
| ⚫ | |||
| + | |||
| ⚫ | |||
| ⚫ | |||
is considered by the special request from [[Sheldon Levenstein]]. |
is considered by the special request from [[Sheldon Levenstein]]. |
||
For this base, tetration was believed to be especially difficult to evaluate. |
For this base, tetration was believed to be especially difficult to evaluate. |
||
| − | The evaluation uses almost the same algorithm of the Cauchi integral <ref name=analuxp> |
+ | The evaluation uses almost the same algorithm of the [[Cauchi integral]] <ref name=analuxp> |
| − | + | https://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html <br> |
|
| − | + | https://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf |
|
| ⚫ | |||
| − | http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf |
||
| ⚫ | |||
</ref>. |
</ref>. |
||
| − | The small modification had been applied to the original algorithm; the condition |
+ | The small modification had been applied to the original algorithm; the condition \(F(z^*)=F(z)^*\) is suppressed at the numerical solving of the corresponding integral equation for values o superfunction along \(\Im(z)=\mathrm{const}\). No difficulties, specific namely for this complex value of base \(b\), had been revealed. |
==Book== |
==Book== |
||
| − | The maps are plotted |
+ | The maps are plotted with the [[conto.cin]] code in [[C++]]. The [[Latex]] codes are used to add the labels. |
All the maps at right are supplied with generators; the colleagues may download the code and reproduce them. |
All the maps at right are supplied with generators; the colleagues may download the code and reproduce them. |
||
If some generator does not work as expected, let me know and let us correct it. |
If some generator does not work as expected, let me know and let us correct it. |
||
| − | The algorithms, used to evaluate the tetration, are described in |
+ | The algorithms, used to evaluate the [[tetration]], are described in Book «[[Superfunctions]]» |
| + | <ref name="br"> |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| + | Dmitrii Kouznetsov. [[Superfunctions]]. [[Lambert Academic Publishing]], 2020. |
||
| + | </ref>, 2020<br> |
||
| + | and also in the Russian version «[[Суперфункции]]» |
||
| + | <ref name="be"> |
||
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br> |
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br> |
||
| − | + | https://mizugadro.mydns.jp/BOOK/202.pdf |
|
| − | http://mizugadro.mydns.jp/BOOK/202.pdf |
||
Д.Кузнецов. Суперфункции. [[Lambert Academic Publishing]], 2014. |
Д.Кузнецов. Суперфункции. [[Lambert Academic Publishing]], 2014. |
||
| − | </ref>. |
+ | </ref>, 2014. |
| + | == Reuse == |
||
| − | For year 2014, the English version is not yet ready. |
||
| + | The [[explicit plot]] and the [[complex map]]s above are supplied with the generators. |
||
| + | |||
| + | The colleagues are invited to download these generators, to reproduce the pictures and to modify them adopting for the new needs. |
||
| + | |||
| + | At the reuse, please, attribute the source and indicate the modification, if any.<br> |
||
| + | This helps to trace the [[bug]]s, if any. |
||
| + | |||
| + | 2016-2018, [[William Paulsen]] and [[Samuel Cowgill]] suggest |
||
| + | an alternative algorithm for evaluation of [[tetration]] to general base \(b\) |
||
| + | <ref> https://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving F(z + 1) = b F(z) in the complex plane. [[Advances in Computational Mathematics]], December 2017, Volume 43, Issue 6, pp 1261–1282 |
||
| + | </ref><ref> |
||
| + | https://search.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750&diss=y Cowgill, Samuel. Exploring Tetration in the Complex Plane. [[Arkansas State University]], ProQuest Dissertations Publishing, 2017. 10263680. |
||
| + | </ref><ref> |
||
| + | https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. [[Advances in Computational Mathematics]], 2018.06.02. |
||
| ⚫ | |||
| + | These results are not supplied with the C++ implementations and not represented here. |
||
==References== |
==References== |
||
| + | {{ref}} |
||
| − | <references/> |
||
| + | |||
| + | {{fer}} |
||
==Keywords== |
==Keywords== |
||
| − | [[Ackermann]] |
+ | «[[Ackermann]]», |
| − | [[Complex map]] |
+ | «[[Complex map]]», |
| + | «[[Superfunction]]», |
||
| ⚫ | |||
| + | «[[Superfunctions]]», |
||
| ⚫ | |||
| + | |||
| ⚫ | |||
[[Category:Ackermann]] |
[[Category:Ackermann]] |
||
| Line 107: | Line 144: | ||
[[Category:BookMap]] |
[[Category:BookMap]] |
||
[[Category:Latex]] |
[[Category:Latex]] |
||
| + | [[Category:Tetration]] |
||
Latest revision as of 13:42, 3 January 2026
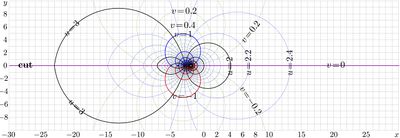
 Base \(b=\sqrt{2}\approx 1.41\)]]
Base \(b=\sqrt{2}\approx 1.41\)]]
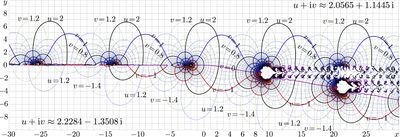
 Henryk base, \(b=\exp(1/\mathrm e)\approx 1.44\)
Henryk base, \(b=\exp(1/\mathrm e)\approx 1.44\)
 Natural base, \(b=\mathrm e \approx 2.71\)
Natural base, \(b=\mathrm e \approx 2.71\)
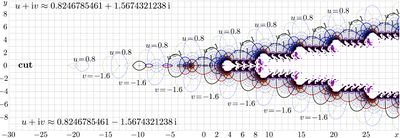
 Sheldon base, \(b=1.52598338517+0.0178411853321 \,\mathrm i\)
Sheldon base, \(b=1.52598338517+0.0178411853321 \,\mathrm i\)
Article Maps of tetration collects some explicit plots and complex maps of tetration \(\mathrm{tet}_b\) to various values of base \(b\).
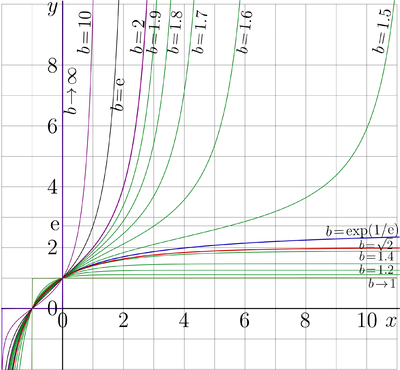
For real values of base \(b\), the real-real plots \(y\!=\!\mathrm{tet}_b(x)\) are shown in the upper figure at right.
Below, the complex maps are shown. The following cases are represented:
\(b=\sqrt{2} \approx 1.41\)
\(b=\exp(1/\mathrm e) \approx 1.44\)
\(b=1.5\)
\(b=2\)
\(b=\mathrm e \approx 2.71\)
\(b=1.52598338517+0.0178411853321 \,\mathrm i\)
Tetration tet is shown with lines of constant real part \(u\) and lines of constant imaginary part \(v\); \(u\!+\!\mathrm i v=\mathrm {tet}_b(x\!+\!\mathrm i y)\)
b=sqrt(2)
For this case, the regular iteration at fixed point \(L=2\) is used. The evaluation is described in the Mathematics of Computation [3].
b= e^(1/e) (approximately 1.44)
For \(b=\exp(1/\mathrm e)\approx 1.44\), the exotic iteration at fixed point \(L=\mathrm e\approx 2.71\) is used. The evaluation is described at the Mathematics of Computation [4], 2012.
b > e^(1/e)
For \(b>\exp(1/\mathrm e)\approx 1.44\), the Cauchi integral is used for evaluation. It is described in Mathematics of Computation [5].
Historically, evaluation for the case \(b=\mathrm e\) was first to be reported. Namely for this case, the special code fsexp.cin is loaded; it is described in Vladikavkaz Mathematical Jorunal [6].
The same algorithm can be used also for other values of base; in particular, for \(b=1.5\) and for \(b=2\); these cases are shown in figures at right.
Sheldon base b=1.52598338517+0.0178411853321 i
Tetration to Sheldon base \(b\!=\!1.52598338517\!+\!0.0178411853321\mathrm i\) is considered by the special request from Sheldon Levenstein. For this base, tetration was believed to be especially difficult to evaluate.
The evaluation uses almost the same algorithm of the Cauchi integral [5].
The small modification had been applied to the original algorithm; the condition \(F(z^*)=F(z)^*\) is suppressed at the numerical solving of the corresponding integral equation for values o superfunction along \(\Im(z)=\mathrm{const}\). No difficulties, specific namely for this complex value of base \(b\), had been revealed.
Book
The maps are plotted with the conto.cin code in C++. The Latex codes are used to add the labels. All the maps at right are supplied with generators; the colleagues may download the code and reproduce them. If some generator does not work as expected, let me know and let us correct it.
The algorithms, used to evaluate the tetration, are described in Book «Superfunctions»
[2], 2020
and also in the Russian version «Суперфункции»
[1], 2014.
Reuse
The explicit plot and the complex maps above are supplied with the generators.
The colleagues are invited to download these generators, to reproduce the pictures and to modify them adopting for the new needs.
At the reuse, please, attribute the source and indicate the modification, if any.
This helps to trace the bugs, if any.
2016-2018, William Paulsen and Samuel Cowgill suggest an alternative algorithm for evaluation of tetration to general base \(b\) [7][8][9]. These results are not supplied with the C++ implementations and not represented here.
References
- ↑ 1.0 1.1
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
https://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014. - ↑ 2.0 2.1 https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
- ↑
https://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
https://mizugadro.mydns.jp/PAPERS/2010q2.pdf D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. - ↑
https://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf
https://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf
https://mizugadro.mydns.jp/PAPERS/2011e1e.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation, 2012, v.81, p.2207-2227. ISSN 1088-6842(e) ISSN 0025-5718(p) - ↑ 5.0 5.1
https://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
https://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, 2009, v.78, p.1647-1670. - ↑ https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑ https://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving F(z + 1) = b F(z) in the complex plane. Advances in Computational Mathematics, December 2017, Volume 43, Issue 6, pp 1261–1282
- ↑ https://search.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750&diss=y Cowgill, Samuel. Exploring Tetration in the Complex Plane. Arkansas State University, ProQuest Dissertations Publishing, 2017. 10263680.
- ↑ https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics, 2018.06.02.
Keywords
«Ackermann», «Complex map», «Superfunction», «Superfunctions», «Tetration»,
«Суперфункции»,