Difference between revisions of "Sandbox"
(version by ChatGPT) |
(rewrote version for "tetration") |
||
| Line 1: | Line 1: | ||
{{top}} |
{{top}} |
||
| + | <div class="thumb tright" style="float:right; margin:-72px 0px 8px 18px"> |
||
| − | |||
| + | {{pic|Tetreal10bx10d.png|300px}} |
||
| − | '''Tetration''' is the superfunction of the [[exponential]] map. |
||
| + | <small><center>\(y=\mathrm{tet}_b(x)\) versos \(x\) for various values of base \(b\).<br> |
||
| + | [[Superfunctions]]<ref name="en"/>, Fig.17.2, p.239.</center></small> |
||
| + | </div> |
||
| + | <div class="thumb tright" style="float:right; background-color:#fff; margin:2px 0px 8px 8px; width:300px; line-height:9px"> |
||
| + | {{pic|Ackerplot.jpg|300px}}<small><center>First five [[ackermann]]s.<!-- [[Natural tetration]] |
||
| + | refers to dashed line.!--><br>[[Superfunctions]]<ref name="en"> |
||
| + | https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862<br> |
||
| + | https://mizugadro.mydns.jp/BOOK/468.pdf |
||
| + | Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28 |
||
| + | </ref>, p.266. Fig.19.7. |
||
| + | </div> |
||
| + | <div class="thumb tright" style="float:right; margin:8px 0px 14px 12px; background-color:#fff; width:220px; line-height:11px;"> |
||
| + | {{pic|B271t.png|240px}}<small><center>Map of [[natural tetration]]. |
||
| + | See Figure 4.12 at page 203 of book [[Superfunctions]]<ref name="en"/></center></small> |
||
| + | </div> |
||
| + | [[Tetration]] ([[Тетрация]]) is the [[superfunction]] of the [[exponential]] map. |
||
For a given base \(b\), the tetration \(\operatorname{tet}_b\) is defined as the function satisfying the transfer equation |
For a given base \(b\), the tetration \(\operatorname{tet}_b\) is defined as the function satisfying the transfer equation |
||
\[ |
\[ |
||
\operatorname{tet}_b(z+1) = b^{\operatorname{tet}_b(z)} |
\operatorname{tet}_b(z+1) = b^{\operatorname{tet}_b(z)} |
||
\] |
\] |
||
| − | together with additional normalization and regularity conditions that select a unique solution among infinitely many possible superfunctions. |
+ | together with additional normalization and regularity conditions that select a unique solution among infinitely many possible superfunctions. |
| + | For real values of the argunet, the explicit plots of \(\operatorname{tet}_b(x)\) versos \(x\) |
||
| + | for various real values of base \(b\) is shown in figure at right. |
||
| + | The inverse function [[ArcTetration]] is denoted with symbol ate; \( \mathrm{ate}_b = \mathrm{tet}_b^{-1} \).<br> |
||
| − | The name “tetration’’ reflects its role as the next operation after exponentiation within the [[hyperoperation]] hierarchy. |
||
| + | The iterates of [[Exponential]] can be expressed as follows: |
||
| + | \( |
||
| + | \exp_b^{\ n}=\operatorname{tet}_b\big(n+\operatorname{ate}_b(z)\big) |
||
| + | \). |
||
| + | Here, number \(n\) of the iterate has no need to be integer. In particular, \(\varphi=\exp^{1/2}\) |
||
| + | appears as solution of equation \( \varphi(\varphi(x))=\mathrm e^x \); this equation had been considered by [[Hellmuth Kneser]] <ref name="k"> |
||
| + | http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi |
||
| + | [[Hellmuth Kneser]]. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. |
||
| + | Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67 |
||
| + | </ref>, 1950. |
||
| + | ==Notations== |
||
| − | The most studied case is the real holomorphic tetration to base \(b=\mathrm e\), written simply as |
||
| + | |||
| + | The name [[tetration]] reflects its role as the next operation after exponentiation within the [[hyperoperation]] hierarchy:<br> |
||
| + | [[Ackermann]]\(_1\), id est, the [[Addition]] appears as [[superfunction]] of [[unity increment]];<br> |
||
| + | [[Ackermann]]\(_2\), id est, the [[Multiplication]] appears as [[superfunction]] of additon; <br> |
||
| + | [[Ackermann]]\(_3\), id est, the [[Exponential]] \(\exp\) appears as [[superfunction]] of multiplication;<br> |
||
| + | [[Ackermann]]\(_4\), id est, the [[Tetration]] \(\mathrm{tet}\) appears as [[superfunction]] of [[exponential]];<br> |
||
| + | [[Ackermann]]\(_5\), id est, the [[Pentation]] \(\mathrm{pen}\) appears as [[superfunction]] of [[tetration]];<br> |
||
| + | and so on. These functions are qualified as [[ackermann]]s after the last name of |
||
| + | mathematician [[Wilhelm Ackermann]]. |
||
| + | |||
| + | The most studied case is the [[Natural tetration]] |
||
| + | <ref name="analuxp"> |
||
| + | https://www.ams.org/journals/mcom/2009-78-267/S0025-5718-09-02188-7/home.html <br> |
||
| + | http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf |
||
| + | Dmitrii Kouznetsov. Solution of F(z+1)=exp(F(z)) in complex z-plane. |
||
| + | Mathematics of Computation, 2009, V.78, p.1647-1670. |
||
| + | </ref><ref name="vladi"> |
||
| + | https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf<br> |
||
| + | https://www.vmj.ru/articles/2010_2_4.pdf <br> |
||
| + | https://mizugadro.mydns.jp/PAPERS/2010_2_4.pdf |
||
| + | D.Kouznetsov. Tetration as special function. (In Rusian) [[Vladikavkaz Mathematical Journal]], 2010, v.12, issue 2, p.31-45. |
||
| + | </ref>. It corresponds to base \(b=\mathrm e\); it can be written simply as |
||
\[ |
\[ |
||
\operatorname{tet}(z)=\operatorname{tet}_{\mathrm e}(z). |
\operatorname{tet}(z)=\operatorname{tet}_{\mathrm e}(z). |
||
\] |
\] |
||
| + | For base \(\mathrm e\) the first five [[ackermann]]s are shown in figure at right.<br> |
||
| + | The dashed line refers to the [[natural tetration]]. |
||
| + | In such a way, all the [[ackermann]]s are numerated. <br> |
||
| − | <div class="thumb tright" style="float:right; margin:-7px 0px 8px -8px"> |
||
| + | In notation [[Ackermann]]\(_m (z)\), the number \(m\) is supposed to be positive integer (natural number). <br> |
||
| − | {{pic|Tetreal10bx10d.png|300px}} |
||
| + | To year 2025, the generalization of [[Ackermann]]\(_m(z)\) for non-integer values of \(m\) is not yet developed. |
||
| − | <small><center>Real tetration to base \(b=\mathrm e\).<br> |
||
| + | However, the argument \(z\) may have complex values. |
||
| − | From: Fig.17.2, p.239 in ''Superfunctions''.</center></small> |
||
| − | </div> |
||
==Definition== |
==Definition== |
||
| + | |||
Let \(T_b(z)=b^z\). |
Let \(T_b(z)=b^z\). |
||
| − | A function \(F\) is a ''superexponential'' (a superfunction of \(T_b\)) if |
+ | A function \(F\) is a ''[[superexponential]]'' (a [[superfunction]] of \(T_b\)) if |
\[ |
\[ |
||
F(z+1) = T_b(F(z)). |
F(z+1) = T_b(F(z)). |
||
\] |
\] |
||
| − | A |
+ | A [[tetration]] to real base \(b\) is real-holomorphic superexponential \(F\) |
| + | such that \(F(x+\mathrm i y)\) remains bounded at \(y\to\pm\infty\) and \(F(0)=1\). |
||
| + | Such a solution is believed to exists and to be unique <ref> |
||
| − | # the limits |
||
| + | https://link.springer.com/article/10.1007/s00010-010-0021-6 |
||
| − | \[ |
||
| + | https://mizugadro.mydins.jp/2011uniabel.pdf |
||
| − | \lim_{y\to\pm\infty} F(x+\mathrm i y) |
||
| + | H.Trappmann, D.Kouznetsov. Uniqueness of holomorphic Abel functions at a complex fixed point pair. |
||
| − | \] |
||
| + | [[Aequationes Mathematicae]], v.81, p.65-76 (2011) |
||
| − | remain finite (regularity at the imaginary infinities), |
||
| + | </ref><ref> |
||
| − | # the normalization |
||
| + | https://math.stackexchange.com/questions/284868/uniqueness-of-tetration |
||
| − | \[ |
||
| − | + | Let 𝑓(0)=1 |
|
| + | and 𝑓(𝑥+1)=2^𝑓(𝑥) // |
||
| − | \] |
||
| + | Also let f be infinitely differentiable. Then does f exist and is it unique? // |
||
| − | holds. |
||
| + | If f is merely continuous, then any continuous function such that f(0)=1 f(1)=2 satisfies the conditions(if f is defined in [0,1] ,we can use the property to define it everywhere else). Similar things can be said for differentiability. But I don't how to solve the problem if it's infinitely differentiable. |
||
| + | </ref>. |
||
| + | ==Special cases== |
||
| − | These conditions remove the otherwise infinite freedom in solutions to the transfer equation. |
||
| + | <div class="thumb tright" style="float:right; margin:-6px 0px 4px 8px; background-color:#fff; width:480px; line-height:8px;"> |
||
| + | {{pic|E1efig09abc1a150.png|480px}}<small><center>[[Complex map]]s of [[tetration]] \(\mathrm{tet}_b\) to base \(b\!=\!1.5\) , left; \(b\!=\!\exp(1/\mathrm e)\) , center and \(b\!=\!\sqrt{2}\) , right.<br> |
||
| + | From: Fig.17.4, p.245 in [[Superfunctions]] <ref name="en"/></center></small> |
||
| + | </div> |
||
| + | <div class="thumb tright" style="float:right; margin:4px 0px 8px 8px"> |
||
| + | {{pic|Tetsheldonmap03.png|480px}}<small><center>[[Tetration to Sheldon base]]. [[Superfunctions]], p.250, top picture of Fig.18.3.</center></small> |
||
| + | </div> |
||
| + | [[Decimal tetration]], \(b=10\). The routine for the evaluation is loaded as [[F4ten.cin]]. |
||
| − | ==Properties== |
||
| + | It is used to plot the top picture. |
||
| − | For the principal tetration \(\operatorname{tet}_b\): |
||
| + | [[Natural tetration]], \(b=\mathrm e\). The [[complex map]] for this case is shown in figure above. The original description <ref name="analuxp"/> and the fast C++ implementation <ref name=vladie"> |
||
| − | * **Transfer equation** |
||
| + | https://www.emis.ams.org/journals/VMJ/articles/2010_2_4.pdf <br> |
||
| − | \[ |
||
| + | https://mizugadro.mydns.jp/PAPERS/2010_2_4.pdf<br> |
||
| − | \operatorname{tet}_b(z+1)=b^{\operatorname{tet}_b(z)}. |
||
| + | https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf<br> |
||
| − | \] |
||
| + | Д.Кузнецов. Тетрация как специальная функция. Владикавказский математический журнал, 2010, т.12, вып. 2, стр.31-45.<br> |
||
| + | D.Kouznetsov, Tetration as special function. Vladikavkaz Mathematical Journal, 2010, |
||
| + | v.12, Issue 2, p.33-45. |
||
| + | </ref> are published and mentioned in book [[Superfunctions]] <ref name="en"/> |
||
| + | [[Binary tetration]], \(b=2\), see [[Base 2]] |
||
| − | * **Derivative at the fixed point** |
||
| − | Let \(L\) satisfy \(L = b^L\). Then |
||
| − | \[ |
||
| − | \operatorname{tet}_b'(0)=L. |
||
| − | \] |
||
| + | [[tetration to base 1.5]], see [[Base 1.5]] |
||
| − | * **Analyticity** |
||
| − | For \(1 < b < \mathrm e^{1/\mathrm e}\), the tetration to base \(b\) extends to an entire function. |
||
| − | For \(b > \mathrm e^{1/\mathrm e}\), branch singularities appear, and a global entire tetration is impossible. |
||
| + | [[Crytical tetration]], \(b= \mathrm e^{1/\mathrm e}\), see [[Base e1e]] |
||
| − | ==Regularity in the base== |
||
| − | The tetration depends smoothly on the base \(b\) for |
||
| − | \[ |
||
| − | 1 < b < \mathrm e^{1/\mathrm e}. |
||
| − | \] |
||
| − | Within this range, the exponential map \(z\mapsto b^z\) has two attracting fixed points, allowing construction of an entire Abel function and an entire tetration. |
||
| + | [[Tetration to base sqrt2]], \(b= \sqrt{2}\), see [[Base sqrt2]] |
||
| − | At the critical base, the two fixed points merge, and the dynamical structure changes. |
||
| − | + | [[Tetration to Sheldon base]] \(b=1.52598338517+0.0178411853321\ \mathrm i\). |
|
| + | The original algorithm <ref name="analuxp"/> allows the straight-forward generalization for the case of complex values of base \(b\). After the request by [[Sheldon Levenstain]], the complex map of this tetration had been generated; it is shown in figure at right. |
||
| − | The point |
||
| − | \[ |
||
| − | b = \frac{1}{\mathrm e} |
||
| − | \] |
||
| − | is a branch point of the exponential map in the parameter \(b\). |
||
| − | Although tetration is smooth for \(b>1/\mathrm e\), this regularity does *not* guarantee holomorphic extendability across the branch point. |
||
| + | ==Continuity at base b=exp(1/e)== |
||
| − | Important observations: |
||
| + | <div class="thumb tright" style="float:right; margin:0 0 8px 8px; width:280px; line-height:10px"> |
||
| + | {{pic|BlackSheep.png|280px}} |
||
| + | <small><center>"half-sheep" illustration. [[Суперфункции]]<ref name="ru"> |
||
| + | https://mizugadro.mydns.jp/BOOK/202.pdf |
||
| + | Дмитрий Кузнецов. [[Суперфункции]]. [[Lambert Academic Publishing]], 2014 |
||
| + | </ref>, p.218, Fig.15.6; [[Superfunctions]] <ref name="en"/>, p.215, Fig.15.6</center></small> |
||
| + | </div> |
||
| + | This cartoon at right illustrates a philosophical point in tetration theory:<br> |
||
| − | * When the base parameter \(b\) is continued into the complex plane, the behavior around \(b=1/\mathrm e\) becomes path-dependent. |
||
| + | <b>"The only we may conclude, that in this county, there is at least one sheep, |
||
| − | * Continuation of tetration above and below the branch point generally does not give the same result — the continuation is multivalued. |
||
| + | and at least the right-hand side of this animal is black"</b>. <br> |
||
| − | * The situation is analogous to the relation between the [[Exponential integral]] \(\operatorname{Ei}\) and \(E_1\): one can smoothly approach the singularity from either side, but no single global holomorphic branch exists. |
||
| + | The heuristic assumptions that appear “obvious’’ (e.g., that the right side of a sheep has the same color as its left side) appears without rigorous proof and, from point of a mathematician, may happen to be wrong. |
||
| − | * For tetration, the complication is deeper because the function depends on two variables \((b,z)\); nonetheless, \(b=1/\mathrm e\) remains a limiting point for the tetrations defined on both sides. |
||
| + | The similar heuristic assumption refers to the continuity of [[tetration]] \(\mathrm{tet}_b(z) \) being considered as function of base \(b\) at point \(b=\exp(1/\mathrm e)\). |
||
| − | This is one of the important unresolved structural problems of tetration theory. |
||
| + | The maps above for \(b=1.5\), \(b=\exp(1/\mathrm e)\approx 1.44\) and \(b=\sqrt{2}\approx 1.41\) |
||
| − | ==Complex structure== |
||
| + | as well as the explicit plot at the top make an impression, that the [[tetration]] is continuous and perhaps holomorphic with respect to \(b\) at this point: the variation in the 3d significant figure causes small change of the view of the curves; at least for moderate valies of argument \(z\) |
||
| − | <div class="thumb tright" style="float:right; margin:0 0 8px 8px"> |
||
| − | {{pic|Ackerplot.jpg|300px}} |
||
| − | <small><center>Ackermann-family functions. |
||
| − | Natural tetration (dashed) and other Ackermann-like functions.<br> |
||
| − | From: Fig.19.7, p.266 in ''Superfunctions''.</center></small> |
||
| − | </div> |
||
| + | As in the case of the sheep in the cartoon, this assumptions about tetration |
||
| − | The complex analytic structure of tetration is governed by the dynamics of \(z\mapsto b^z\). |
||
| + | is not obvious and require careful justification. |
||
| − | For \(1<b<\mathrm e^{1/\mathrm e}\), the map has two attracting fixed points. |
||
| − | This allows one to construct an Abel function that is analytic on the entire plane and thus an entire tetration. |
||
| + | The prelimninary numerical analysis indicates, that |
||
| − | At the critical base \(b=\mathrm e^{1/\mathrm e}\), the two fixed points collide (parabolic bifurcation). |
||
| + | \(tet_b(z)\) for \(\Re(b)<\exp(1/\mathrm e)\) |
||
| − | For \(b>\mathrm e^{1/\mathrm e}\), both fixed points become repelling, and the Abel function — hence tetration — develops branch points and cannot be entire. |
||
| + | is not analytical extension of |
||
| + | \(tet_b(z)\) for \(\Re(b)>\exp(1/\mathrm e)\); |
||
| + | in the simplest way, the cut line along line \(\Re(b)=\exp(1/\mathrm e)\) |
||
| + | divides the complex plane to two almost independent parts, |
||
| + | and only in point \(Re(b)=\exp(1/\mathrm e)\), these two tetrqations have the same limiting |
||
| + | tetration. <br> |
||
| + | However, the cut at the complex \(b\)-plane has no need to follow the vertical line \(\Re(b)=\exp(1/\mathrm e)\); but this choice is simplest and has priority (following the last, 6th of the [[TORI axioms]].) |
||
| + | ==Applications== |
||
| − | ==Relation to superfunctions== |
||
| + | The obvious application of the tetration may refer to representation of huge numbers.<br> |
||
| − | A superfunction \(F\) of \(T_b\) satisfies |
||
| + | For example the [[Googolplex]] number <ref> |
||
| + | https://en.wikipedia.org/wiki/Googolplex |
||
| + | A '''googolplex''' is the [[large number]] \(10^{10^{100}}\), that is, 10 raised to the power of a [[googol]]. If written out in ordinary [[decimal notation]], it would be 1 followed by a [[googol]] (10<sup>100</sup>) zeroes – a physically impossible number to write explicitly. |
||
| + | </ref> can be expressed as follows: |
||
\[ |
\[ |
||
| + | 10^{10^{100}}=\mathrm{tet}_{10}^3(2) |
||
| − | F(z+1)=b^{F(z)}. |
||
\] |
\] |
||
| + | However, up to year 2025, Editor have not yet found any [[scientific concept]] |
||
| + | that deals with such a huge number. |
||
| + | The additional application may refer to the approximation of processes that |
||
| − | Among the infinitely many such functions, the tetration is selected by: |
||
| + | grows faster than any polynomial but slower than any exponential. |
||
| + | The non-inteher iterates greatly extend the arsenal of functions available for |
||
| + | construction of efficient fits, involving less fitting parameters and/or providing better precision and/or having wider range of approximation. |
||
| + | The \(n\)-th iterate of the exponential: |
||
| − | * realness on the real axis, |
||
| − | * holomorphy in a vertical strip, |
||
| − | * regularity at \(+\mathrm i\infty\) and \(-\mathrm i\infty\), |
||
| − | * normalization at \(z=0\). |
||
| − | |||
| − | All other superexponentials differ by periodic or quasiperiodic distortions. |
||
| − | |||
| − | ==Inverse: Abel function== |
||
| − | The inverse of tetration is the [[Abel function]] (ArcTetration), denoted \(\operatorname{ate}_b\). |
||
| − | It satisfies |
||
\[ |
\[ |
||
| − | \ |
+ | \exp_b^{\ n}(z) = \operatorname{tet}_b\!\big(n + \operatorname{ate}_b(z)\big), |
| − | \] |
||
| − | with |
||
| − | \[ |
||
| − | \operatorname{ate}_b(1)=0. |
||
\] |
\] |
||
| + | for real \(n\). One example of such a function is mentioned in the Preamble. |
||
| + | An additional extension could be generalization of [[ackermann]]\(m\) |
||
| − | For the natural exponential: |
||
| + | to non-integer values of \(m\), looking for the real-holomorphic solition \(A\) of equations |
||
\[ |
\[ |
||
| + | A_m(z+1)=A_{m-1}(A_m(z)) \\ |
||
| − | \operatorname{ate}(\exp(z)) = \operatorname{ate}(z) + 1. |
||
| + | A_2(z)= \mathrm e\ z \\ |
||
| + | Z_m(0)=1 \text{ for } m>2 |
||
\] |
\] |
||
| + | treating \(A_m(z)\) as holomorphic function of two variables \(m\) and \(z\).<br> |
||
| + | Such a generalization can be matter for the future research. |
||
| − | == |
+ | ==References== |
| + | {{ref}} |
||
| − | Tetration and ArcTetration provide analytic extensions of integer iteration. |
||
| − | For the \(n\)-th iterate of the exponential: |
||
| − | \[ |
||
| − | \exp_b^n(z) = \operatorname{tet}_b\!\big(n + \operatorname{ate}_b(z)\big), |
||
| − | \] |
||
| − | valid for real or complex \(n\). |
||
| + | https://www.numdam.org/item?id=BSMF_1919__47__161_0 |
||
| − | ==Special cases== |
||
| + | P. Fatou. Sur les ´equations fonctionnelles. Bulletin de la Soci´et´e |
||
| − | <div class="thumb tright" style="float:right; margin:-30px 0 8px 8px"> |
||
| + | Math´ematique de France, 47 (1919), p. 161-271. |
||
| − | {{pic|E1efig09abc1a150.png|480px}} |
||
| − | <small><center>Tetration near the critical base \(b=\mathrm e^{1/\mathrm e}\).<br> |
||
| − | From: Fig.17.4, p.245 in ''Superfunctions''.</center></small> |
||
| − | </div> |
||
| + | https://eretrandre.org/rb/files/Ackermann1928_126.pdf |
||
| − | ===Base \(\sqrt{2}\)=== |
||
| + | Wilhelm Ackermann. Zum Hilbertschen Aufbau der reellen Zahlen. [[Mathematische Annalen]] 99, Number 1(1928), Z.118-133. |
||
| − | A classical example of an entire tetration, used extensively in early numerical work. |
||
| + | <small>https://projecteuclid.org/journals/acta-mathematica/volume-100/issue-3-4/Regular-iteration-of-real-and-complex-functions/10.1007/BF02559539.full |
||
| − | ===Base \(b= \mathrm e^{1/\mathrm e}\)=== |
||
| + | </small> |
||
| − | This “critical base’’ marks the transition where the fixed points of \(z\mapsto b^z\) merge. |
||
| + | G.Szekeres. Regular iteration of real and complex functions. Acta Mathematica 1958, Volume 100, Issue 3-4, pp 203-258. |
||
| − | Properties include: |
||
| + | https://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf |
||
| − | * extremely slow growth near the fixed point, |
||
| + | W.Bergweiler. Iteration of meromorphic functions. Bulletin (New Series) of the American Mathematical society, v.29, No.2 (1993) p.151-188. |
||
| − | * non-entire analytic continuation, |
||
| − | * delicate dependence on initial conditions. |
||
| + | https://www.tandfonline.com/doi/full/10.1080/10652460500422247 |
||
| − | ===Base 2=== |
||
| + | M.H.Hooshmand, (2006). Ultra power and ultra exponential functions. Integral [[Transforms and Special Functions]] 17 (8): 549–558 |
||
| − | An important superexponential used in comparisons with hyperoperators. |
||
| + | https://www.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750 |
||
| − | ===Natural tetration=== |
||
| + | [[Samuel Cowgill]]. EXPLORING TETRATION IN THE COMPLEX PLANE |
||
| − | The principal tetration \(\operatorname{tet}(z)\) is real-analytic on the real axis. |
||
| + | EXPLORING TETRATION IN THE COMPLEX PLANE |
||
| − | As \(z\to -\infty\), it approaches the lower fixed point of \(\exp(z)\). |
||
| + | A Thesis presented to the faculty of Arkansas State University in partial. |
||
| − | As \(z\to +\infty\), it grows faster than any finite exponential tower. |
||
| + | fulfillment of the requirements for the Degree of |
||
| + | MASTER OF SCIENCE IN MATHEMATICS |
||
| + | ARKANSAS STATE UNIVERSITY //MAY 2017 |
||
| + | Approved by: |
||
| + | Dr. [[William Paulsen]], Thesis Advisor |
||
| + | Dr. [[Jie Miao]], Committee Member |
||
| + | Dr. [[Jeongho Ahn]], Committee MemberPREVIE |
||
| + | https://link.springer.com/article/10.1007/s10444-018-9615-7 |
||
| − | ==Figures== |
||
| + | William Paulsen. Tetration for complex bases. |
||
| − | <div class="thumb tright" style="float:right; margin:0 0 8px 8px"> |
||
| + | Advances in Computational Mathematics. |
||
| − | {{pic|B271t.png|300px}} |
||
| + | Published: 02 June 2018// |
||
| − | <small><center>Tetration and its inverse (ArcTetration).<br> |
||
| + | Volume 45, pages 243–267, (2019) |
||
| − | From: Fig.14.4, p.203 in ''Superfunctions''.</center></small> |
||
| − | </div> |
||
| + | https://www.researchgate.net/publication/325532999_Tetration_for_complex_bases |
||
| − | <div class="thumb tright" style="float:right; margin:0 0 8px 8px"> |
||
| + | <br> |
||
| − | {{pic|Tetsheldonmap03.png|300px}} |
||
| + | https://www.researchgate.net/figure/Level-curves-for-Rk-b-z-and-Ik-b-z-0-1-2-3-4-for-b-i_fig1_325532999 |
||
| − | <small><center>Complex structure of tetration.<br> |
||
| + | [[William Harold Paulsen]]. Tetration for complex bases. |
||
| − | From: Fig.18.3 (top), p.250 in ''Superfunctions''.</center></small> |
||
| + | Advances in Computational Mathematics 45(6), |
||
| − | </div> |
||
| + | February 2019 |
||
| + | DOI:10.1007/s10444-018-9615-7 |
||
| + | http://myweb.astate.edu/wpaulsen/tetration2.pdf |
||
| − | ==Conceptual illustration== |
||
| + | [[William Paulsen]] and [[Samuel Cowgil]]. |
||
| − | <div class="thumb tright" style="float:right; margin:0 0 8px 8px"> |
||
| + | Solving F(z+1)=bF(z) in the complex plane. |
||
| − | {{pic|BlackSheep.png|280px}} |
||
| − | <small><center>Heuristic “half-sheep’’ illustration.<br> |
||
| − | From: Fig.15.6, p.218 in ''Суперфункции'' (2014).</center></small> |
||
| − | </div> |
||
| − | |||
| − | This cartoon illustrates a philosophical point in tetration theory: |
||
| − | heuristic assumptions that appear “obvious’’ (e.g., that the right side of a sheep has the same color as the left) may be false without rigorous proof. |
||
| − | |||
| − | Likewise, assumptions about tetration — such as smoothness in both arguments \((b,z)\), or holomorphic extendability across \(b=1/\mathrm e\) — require careful justification. |
||
| − | The cartoon emphasizes that the behavior of superexponentials around their branch points is subtler than it may first appear. |
||
| − | |||
| − | ==References== |
||
| − | {{ref}} |
||
| − | |||
| − | D. Kouznetsov. ''Superfunctions''. Lambert Academic Publishing, 2020. |
||
| − | All cited figures except the last are taken from this monograph. |
||
| − | |||
| − | D. Kouznetsov. ''Суперфункции''. Lambert Academic Publishing, 2014. |
||
| − | Figure 15.6 (the “half-sheep’’) is taken from this edition. |
||
{{fer}} |
{{fer}} |
||
==Keywords== |
==Keywords== |
||
| + | «[[Abel function]]», |
||
| − | «[[Base e1e]]», «[[Base sqrt2]]», «[[Superfunction]]», «[[Exponential]]», «[[Logarithm]]», |
||
| + | «[[ate]]», |
||
| − | «[[Tetration]]», «[[ate]]», «[[Abel function]]», «[[Transfer equation]]», «[[Iterates]]». |
||
| + | «[[Base e1e]]», |
||
| + | «[[Base sqrt2]]», |
||
| + | «[[Exponential]]», |
||
| + | «[[Iterates]]». |
||
| + | «[[Logarithm]]», |
||
| + | «[[Superfunction]]», |
||
| + | «[[Superfunctions]]», |
||
| + | «[[tet]]», |
||
| + | «[[Tetration]]», |
||
| + | «[[Transfer equation]]», |
||
| + | [[Category:English]] |
||
| + | [[Category:Exponential]] |
||
| + | [[Category:Superexponential]] |
||
[[Category:Superfunction]] |
[[Category:Superfunction]] |
||
| − | [[Category: |
+ | [[Category:Superfunctions]] |
[[Category:Special function]] |
[[Category:Special function]] |
||
| − | [[Category: |
+ | [[Category:Tetration]] |
Revision as of 12:00, 13 December 2025
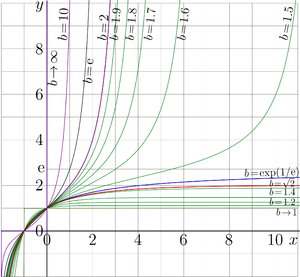
Superfunctions[1], Fig.17.2, p.239.

Superfunctions[1], p.266. Fig.19.7.
Tetration (Тетрация) is the superfunction of the exponential map. For a given base \(b\), the tetration \(\operatorname{tet}_b\) is defined as the function satisfying the transfer equation \[ \operatorname{tet}_b(z+1) = b^{\operatorname{tet}_b(z)} \] together with additional normalization and regularity conditions that select a unique solution among infinitely many possible superfunctions. For real values of the argunet, the explicit plots of \(\operatorname{tet}_b(x)\) versos \(x\) for various real values of base \(b\) is shown in figure at right.
The inverse function ArcTetration is denoted with symbol ate; \( \mathrm{ate}_b = \mathrm{tet}_b^{-1} \).
The iterates of Exponential can be expressed as follows:
\(
\exp_b^{\ n}=\operatorname{tet}_b\big(n+\operatorname{ate}_b(z)\big)
\).
Here, number \(n\) of the iterate has no need to be integer. In particular, \(\varphi=\exp^{1/2}\)
appears as solution of equation \( \varphi(\varphi(x))=\mathrm e^x \); this equation had been considered by Hellmuth Kneser [2], 1950.
Notations
The name tetration reflects its role as the next operation after exponentiation within the hyperoperation hierarchy:
Ackermann\(_1\), id est, the Addition appears as superfunction of unity increment;
Ackermann\(_2\), id est, the Multiplication appears as superfunction of additon;
Ackermann\(_3\), id est, the Exponential \(\exp\) appears as superfunction of multiplication;
Ackermann\(_4\), id est, the Tetration \(\mathrm{tet}\) appears as superfunction of exponential;
Ackermann\(_5\), id est, the Pentation \(\mathrm{pen}\) appears as superfunction of tetration;
and so on. These functions are qualified as ackermanns after the last name of
mathematician Wilhelm Ackermann.
The most studied case is the Natural tetration
[3][4]. It corresponds to base \(b=\mathrm e\); it can be written simply as
\[
\operatorname{tet}(z)=\operatorname{tet}_{\mathrm e}(z).
\]
For base \(\mathrm e\) the first five ackermanns are shown in figure at right.
The dashed line refers to the natural tetration.
In such a way, all the ackermanns are numerated.
In notation Ackermann\(_m (z)\), the number \(m\) is supposed to be positive integer (natural number).
To year 2025, the generalization of Ackermann\(_m(z)\) for non-integer values of \(m\) is not yet developed.
However, the argument \(z\) may have complex values.
Definition
Let \(T_b(z)=b^z\). A function \(F\) is a superexponential (a superfunction of \(T_b\)) if \[ F(z+1) = T_b(F(z)). \]
A tetration to real base \(b\) is real-holomorphic superexponential \(F\) such that \(F(x+\mathrm i y)\) remains bounded at \(y\to\pm\infty\) and \(F(0)=1\).
Such a solution is believed to exists and to be unique [5][6].
Special cases
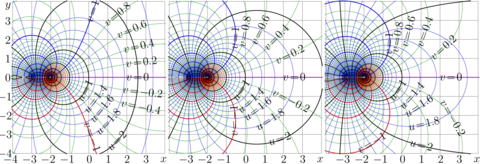
From: Fig.17.4, p.245 in Superfunctions [1]

Decimal tetration, \(b=10\). The routine for the evaluation is loaded as F4ten.cin. It is used to plot the top picture.
Natural tetration, \(b=\mathrm e\). The complex map for this case is shown in figure above. The original description [3] and the fast C++ implementation [7] are published and mentioned in book Superfunctions [1]
Binary tetration, \(b=2\), see Base 2
tetration to base 1.5, see Base 1.5
Crytical tetration, \(b= \mathrm e^{1/\mathrm e}\), see Base e1e
Tetration to base sqrt2, \(b= \sqrt{2}\), see Base sqrt2
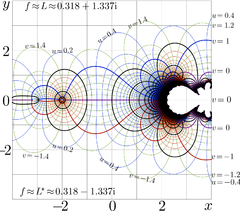
Tetration to Sheldon base \(b=1.52598338517+0.0178411853321\ \mathrm i\). The original algorithm [3] allows the straight-forward generalization for the case of complex values of base \(b\). After the request by Sheldon Levenstain, the complex map of this tetration had been generated; it is shown in figure at right.
Continuity at base b=exp(1/e)
This cartoon at right illustrates a philosophical point in tetration theory:
"The only we may conclude, that in this county, there is at least one sheep,
and at least the right-hand side of this animal is black".
The heuristic assumptions that appear “obvious’’ (e.g., that the right side of a sheep has the same color as its left side) appears without rigorous proof and, from point of a mathematician, may happen to be wrong.
The similar heuristic assumption refers to the continuity of tetration \(\mathrm{tet}_b(z) \) being considered as function of base \(b\) at point \(b=\exp(1/\mathrm e)\).
The maps above for \(b=1.5\), \(b=\exp(1/\mathrm e)\approx 1.44\) and \(b=\sqrt{2}\approx 1.41\) as well as the explicit plot at the top make an impression, that the tetration is continuous and perhaps holomorphic with respect to \(b\) at this point: the variation in the 3d significant figure causes small change of the view of the curves; at least for moderate valies of argument \(z\)
As in the case of the sheep in the cartoon, this assumptions about tetration is not obvious and require careful justification.
The prelimninary numerical analysis indicates, that
\(tet_b(z)\) for \(\Re(b)<\exp(1/\mathrm e)\)
is not analytical extension of
\(tet_b(z)\) for \(\Re(b)>\exp(1/\mathrm e)\);
in the simplest way, the cut line along line \(\Re(b)=\exp(1/\mathrm e)\)
divides the complex plane to two almost independent parts,
and only in point \(Re(b)=\exp(1/\mathrm e)\), these two tetrqations have the same limiting
tetration.
However, the cut at the complex \(b\)-plane has no need to follow the vertical line \(\Re(b)=\exp(1/\mathrm e)\); but this choice is simplest and has priority (following the last, 6th of the TORI axioms.)
Applications
The obvious application of the tetration may refer to representation of huge numbers.
For example the Googolplex number [9] can be expressed as follows:
\[
10^{10^{100}}=\mathrm{tet}_{10}^3(2)
\]
However, up to year 2025, Editor have not yet found any scientific concept
that deals with such a huge number.
The additional application may refer to the approximation of processes that grows faster than any polynomial but slower than any exponential. The non-inteher iterates greatly extend the arsenal of functions available for construction of efficient fits, involving less fitting parameters and/or providing better precision and/or having wider range of approximation.
The \(n\)-th iterate of the exponential: \[ \exp_b^{\ n}(z) = \operatorname{tet}_b\!\big(n + \operatorname{ate}_b(z)\big), \] for real \(n\). One example of such a function is mentioned in the Preamble.
An additional extension could be generalization of ackermann\(m\)
to non-integer values of \(m\), looking for the real-holomorphic solition \(A\) of equations
\[
A_m(z+1)=A_{m-1}(A_m(z)) \\
A_2(z)= \mathrm e\ z \\
Z_m(0)=1 \text{ for } m>2
\]
treating \(A_m(z)\) as holomorphic function of two variables \(m\) and \(z\).
Such a generalization can be matter for the future research.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5
https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862
https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28 - ↑ http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
- ↑ 3.0 3.1 3.2
https://www.ams.org/journals/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf Dmitrii Kouznetsov. Solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, 2009, V.78, p.1647-1670. - ↑
https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf
https://www.vmj.ru/articles/2010_2_4.pdf
https://mizugadro.mydns.jp/PAPERS/2010_2_4.pdf D.Kouznetsov. Tetration as special function. (In Rusian) Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. - ↑ https://link.springer.com/article/10.1007/s00010-010-0021-6 https://mizugadro.mydins.jp/2011uniabel.pdf H.Trappmann, D.Kouznetsov. Uniqueness of holomorphic Abel functions at a complex fixed point pair. Aequationes Mathematicae, v.81, p.65-76 (2011)
- ↑ https://math.stackexchange.com/questions/284868/uniqueness-of-tetration Let 𝑓(0)=1 and 𝑓(𝑥+1)=2^𝑓(𝑥) // Also let f be infinitely differentiable. Then does f exist and is it unique? // If f is merely continuous, then any continuous function such that f(0)=1 f(1)=2 satisfies the conditions(if f is defined in [0,1] ,we can use the property to define it everywhere else). Similar things can be said for differentiability. But I don't how to solve the problem if it's infinitely differentiable.
- ↑
https://www.emis.ams.org/journals/VMJ/articles/2010_2_4.pdf
https://mizugadro.mydns.jp/PAPERS/2010_2_4.pdf
https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf
Д.Кузнецов. Тетрация как специальная функция. Владикавказский математический журнал, 2010, т.12, вып. 2, стр.31-45.
D.Kouznetsov, Tetration as special function. Vladikavkaz Mathematical Journal, 2010, v.12, Issue 2, p.33-45. - ↑ https://mizugadro.mydns.jp/BOOK/202.pdf Дмитрий Кузнецов. Суперфункции. Lambert Academic Publishing, 2014
- ↑ https://en.wikipedia.org/wiki/Googolplex A googolplex is the large number \(10^{10^{100}}\), that is, 10 raised to the power of a googol. If written out in ordinary decimal notation, it would be 1 followed by a googol (10100) zeroes – a physically impossible number to write explicitly.
https://www.numdam.org/item?id=BSMF_1919__47__161_0 P. Fatou. Sur les ´equations fonctionnelles. Bulletin de la Soci´et´e Math´ematique de France, 47 (1919), p. 161-271.
https://eretrandre.org/rb/files/Ackermann1928_126.pdf Wilhelm Ackermann. Zum Hilbertschen Aufbau der reellen Zahlen. Mathematische Annalen 99, Number 1(1928), Z.118-133.
https://projecteuclid.org/journals/acta-mathematica/volume-100/issue-3-4/Regular-iteration-of-real-and-complex-functions/10.1007/BF02559539.full G.Szekeres. Regular iteration of real and complex functions. Acta Mathematica 1958, Volume 100, Issue 3-4, pp 203-258.
https://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf W.Bergweiler. Iteration of meromorphic functions. Bulletin (New Series) of the American Mathematical society, v.29, No.2 (1993) p.151-188.
https://www.tandfonline.com/doi/full/10.1080/10652460500422247 M.H.Hooshmand, (2006). Ultra power and ultra exponential functions. Integral Transforms and Special Functions 17 (8): 549–558
https://www.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750 Samuel Cowgill. EXPLORING TETRATION IN THE COMPLEX PLANE EXPLORING TETRATION IN THE COMPLEX PLANE A Thesis presented to the faculty of Arkansas State University in partial. fulfillment of the requirements for the Degree of MASTER OF SCIENCE IN MATHEMATICS ARKANSAS STATE UNIVERSITY //MAY 2017 Approved by: Dr. William Paulsen, Thesis Advisor Dr. Jie Miao, Committee Member Dr. Jeongho Ahn, Committee MemberPREVIE
https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics. Published: 02 June 2018// Volume 45, pages 243–267, (2019)
https://www.researchgate.net/publication/325532999_Tetration_for_complex_bases
https://www.researchgate.net/figure/Level-curves-for-Rk-b-z-and-Ik-b-z-0-1-2-3-4-for-b-i_fig1_325532999
William Harold Paulsen. Tetration for complex bases.
Advances in Computational Mathematics 45(6),
February 2019
DOI:10.1007/s10444-018-9615-7
http://myweb.astate.edu/wpaulsen/tetration2.pdf William Paulsen and Samuel Cowgil. Solving F(z+1)=bF(z) in the complex plane.
Keywords
«Abel function», «ate», «Base e1e», «Base sqrt2», «Exponential», «Iterates». «Logarithm», «Superfunction», «Superfunctions», «tet», «Tetration», «Transfer equation»,