Difference between revisions of "File:Doya500.png"
(refs, keywords) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{oq|Doya500.png|Doya500.png (153 × 237 pixels, file size: 55 KB, MIME type: image/png)}} |
||
| ⚫ | |||
| + | |||
| ⚫ | |||
| + | |||
| + | Author opens/discovers the [[Superfunctions]]. |
||
[[Complex map]] of the [[Doya function]], rotated counter-clock vice for 90<sup>o</sup>. |
[[Complex map]] of the [[Doya function]], rotated counter-clock vice for 90<sup>o</sup>. |
||
| Line 13: | Line 17: | ||
are shown with thick lines. |
are shown with thick lines. |
||
| + | This map is used as Fig.5.14 at page 58 of book «[[Superfunctions]]» |
||
| + | <ref> |
||
| + | https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other [[superfunction]]s. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28 |
||
| + | </ref><ref>https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other [[superfunction]]s. Formulas, algorithms, tables, graphics. Publisher: [[Lambert Academic Publishing]]. |
||
| + | </ref>. |
||
==[[C++]] generator of the image== |
==[[C++]] generator of the image== |
||
| − | + | //Files [[ado.cin]], [[conto.cin]] and [[doya.cin]] should be loaded for the compillation of the code below. |
|
| + | //<pre> |
||
| − | |||
| − | |||
#include <math.h> |
#include <math.h> |
||
#include <stdio.h> |
#include <stdio.h> |
||
| Line 69: | Line 77: | ||
getchar(); system("killall Preview"); |
getchar(); system("killall Preview"); |
||
} |
} |
||
| + | </pre> |
||
| − | |||
==Copyleft status== |
==Copyleft status== |
||
Copyleft 2011 by Dmitrii Kouznetsov. |
Copyleft 2011 by Dmitrii Kouznetsov. |
||
| Line 75: | Line 83: | ||
(The attribution helps to trace errors if any.) |
(The attribution helps to trace errors if any.) |
||
| + | ==References== |
||
| + | {{ref}} |
||
| + | |||
| + | {{fer}} |
||
| + | ==Keywords== |
||
| + | «[[Doya function]]», |
||
| + | «[[Transferfunction]]», |
||
| + | «[[Superfunctions]]», |
||
| + | |||
| ⚫ | |||
[[Category:Book]] |
[[Category:Book]] |
||
[[Category:BookDraw]] |
[[Category:BookDraw]] |
||
| + | [[Category:BookMap]] |
||
[[Category:C++]] |
[[Category:C++]] |
||
[[Category:Complex map]] |
[[Category:Complex map]] |
||
[[Category:Complex maps]] |
[[Category:Complex maps]] |
||
[[Category:Doya function]] |
[[Category:Doya function]] |
||
| ⚫ | |||
[[Category:Humor]] |
[[Category:Humor]] |
||
| + | [[Category:Superfunctions]] |
||
Latest revision as of 11:55, 19 August 2025
Автор открывает суперфункции.
Author opens/discovers the Superfunctions.
Complex map of the Doya function, rotated counter-clock vice for 90o.
\(f=\mathrm{Doya}_1(y\!+\! \mathrm i x)\) is shown in the \(x,y\) plane with lines \(u\!=\!\Re(f)\!=\!\mathrm{const}\) and lines \(v\!=\!\Im(f)\!=\!\mathrm{const}\).
Levels \(v\!=\!\pm 1.2\), \(v\!=\!\pm 1.4\), \(u\!=\!-0.4\) are shown with thick lines.
This map is used as Fig.5.14 at page 58 of book «Superfunctions» [1][2].
C++ generator of the image
//Files ado.cin, conto.cin and doya.cin should be loaded for the compillation of the code below.
// #include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
#include "doya.cin"
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
int M=230,M1=M+1;
int N=330,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("doya2.eps","w");ado(o,22,34);
fprintf(o,"11 30.5 translate\n 10 10 scale\n");
DO(m,M1) X[m]=-1.1+.01*(m-.5);
DO(n,N1) Y[n]=-3.+.01*(n-.5);
// for(m=-4;m<5;m++){if(m==0){M(m,-4.2)L(m,4.2)} else{M(m,-4)L(m,4)}}
// for(n=-4;n<5;n++){ M( -4,n)L(4,n)}
fprintf(o,".008 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(y,x);
c=Doya(1.,z);
p=Re(c);q=Im(c);
if(p>-99. && p<99. && q>-99. && q<99. ){ g[m*N1+n]=p;f[m*N1+n]=q;}
}}
fprintf(o,"1 setlinejoin 1 setlinecap\n"); p=1.;q=.9;
conto(o,f,w,v,X,Y,M,N,1.2,-q, q); fprintf(o,".1 W 0 .3 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N,-1.2,-q, q); fprintf(o,".1 W 0 .3 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N,1.4,-q, q); fprintf(o,".1 W 0 .3 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N,-1.4,-q, q); fprintf(o,".1 W 0 .3 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,-.4,-q, q); fprintf(o,".1 W .3 0 0 RGB S\n");
for(m=-6;m<5;m++)for(n=1;n<10;n+=1)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q, q); fprintf(o,".003 W 0 .9 0 RGB S\n");
for(m=0;m<6;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q); fprintf(o,".003 W 1 0 0 RGB S\n");
for(m=0;m<6;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q); fprintf(o,".003 W 0 0 1 RGB S\n");
for(m=1;m<5;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".006 W .9 0 0 RGB S\n");
for(m=1;m<5;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".006 W 0 0 .9 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".006 W .6 0 .6 RGB S\n");
for(m=-1;m<2;m++) conto(o,g,w,v,X,Y,M,N, (0.+m ),-p,p); fprintf(o,".003 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf doya2.eps");
system( "open doya2.pdf");
getchar(); system("killall Preview");
}
Copyleft status
Copyleft 2011 by Dmitrii Kouznetsov. The image and the generator may be used for free, but the source should be attributed. (The attribution helps to trace errors if any.)
References
- ↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28
- ↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.
Keywords
«Doya function», «Transferfunction», «Superfunctions»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 | 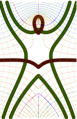 | 153 × 237 (55 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following file is a duplicate of this file (more details):
The following 3 pages use this file: