File:Z2sin1zMapT.png

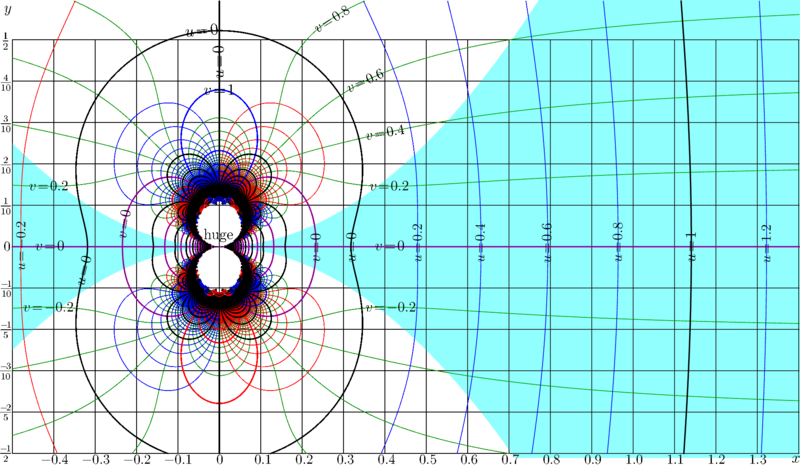
Complex map of function \(f= z \mapsto z^2\sin(1/z) \ \).

Notation: \( u+\mathrm i v = f(x\!+\!\mathrm i y)\ \);

levels \(u=\mathrm{const}\) and

levels \(v=\mathrm{const}\) are drawn.

The restricted asymptotic \( z \mapsto 0\ \) takes place at \( z \to 0 \ , |\Im(z)|<\Re(z)^2\) : \[ \lim_{z\to 0,\ |\Im(z)|<\Re(z)^2 } f(z)=0 \]

Range \(|y|<x^2\) in the map is shaded.

The stricted asymptotic \( z \mapsto z\ \) (that is identity function) takes place at \(\ |z| \to \infty \):

\[ \lim_{z\to \infty } f(z) - z =0 \]

The map is generated using routine Conrec6.cin made with ChatGPT.

In future, routine Conrec6.cin is expected to substitute, to replace its historic analogy conto.cin.

The map is generated as an illustration, as an example of the restricted asymptotic for article «Asymptotic»,
but also as test and demo of routine Conrec6.cin.

C++ generator of contour

/* files ado.cin and Conrec6.cin should be loaded */

// c++ -std=c++11 Z2sin1zMap.cc -O2 -o Z2sin1zMap
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
 #include"ado.cin"
 #define M(x,y) fprintf(o,"%6.4f %6.4f M\n",1.*(x),1.*(y));
 #define L(x,y) fprintf(o,"%6.4f %6.4f L\n",1.*(x),1.*(y));

#include "Conrec6.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
int M=951,M1=M+1;
int N=548,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1];
FILE *o;o=fopen("Z2sin1zMap.eps","w");ado(o,1920,1120);
fprintf(o,"510 510 translate\n 1000 1000 scale\n");

for(n=0;n<192;n++) {x=-.5+.01*n; p=fabs(x); y=p*p; if(n==0) M(x,y) else    L(x,y) }
for(n=200;n>-1;n--){x=-.5+.01*n; p=fabs(x); y=-p*p;  L(x,y) }
fprintf(o,"C .6 1 1 RGB F\n");

DO(m,M1) X[m]=-.5+.002*(m-.2);
DO(n,250)Y[n]=-.5+.002*n;
        Y[250]=-.00001;
        Y[251]= .00001;
for(n=252;n<N1;n++) Y[n]=-.5+.002*(n-1.);

for(m=-5;m<15;m++){M(.1*m,-.5)L(.1*m,.5)}
for(n=-5;n<6;n++){M( -.5,.1*n)L(1.401,.1*n)}
fprintf(o,"2 setlinecap .0012 W 0 0 0 RGB S\n");
//fprintf(o,".0007 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m+M1*n]=9999; f[m+M1*n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); 
// c=Filog(z);
c=z*z*sin(1./z);
p=Re(c);q=Im(c); 
//if(p>-201. && p<201. && q>-201. && q<201. ){ g[m+N1*n]=p;f[m+N1*n]=q;}
if(p>-201. && p<201. && q>-201. && q<201. ){ g[m+M1*n]=p;f[m+M1*n]=q;}
       }}
fprintf(o,"1 setlinejoin 1 setlinecap\n"); p=5.;q=1;

for(m=-10;m<10;m++)for(n=2;n<10;n+=2)Conrec6(o,f,X,Y,M1,N1,(m+.1*n), q); fprintf(o,".0014 W 0 .6 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)Conrec6(o,g,X,Y,M1,N1,-(m+.1*n), q); fprintf(o,".0014 W .9 0 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)Conrec6(o,g,X,Y,M1,N1, (m+.1*n), q); fprintf(o,".0014 W 0 0 .9 RGB S\n");
for(m=1;m<20;m++) Conrec6(o,f,X,Y,M1,N1, (0.-m),p); fprintf(o,".003 W .9 0 0 RGB S\n");
for(m=1;m<20;m++) Conrec6(o,f,X,Y,M1,N1, (0.+m),p); fprintf(o,".003 W 0 0 .9 RGB S\n");
                  Conrec6(o,f,X,Y,M1,N1, (0. ),p); fprintf(o,".003 W .6 0 .6 RGB S\n");
for(m=-20;m<21;m++) Conrec6(o,g,X,Y,M1,N1, (0.+m),p); fprintf(o,".003 W 0 0 0 RGB S\n");

p=10.;
Conrec6(o,g,X,Y,M1,N1, 30 ,p); fprintf(o,".002 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 40 ,p); fprintf(o,".002 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 50 ,p); fprintf(o,".002 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1,-30 ,p); fprintf(o,".002 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1,-40 ,p); fprintf(o,".002 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1,-50 ,p); fprintf(o,".002 W 0 0 0 RGB S\n");
Conrec6(o,f,X,Y,M1,N1,-30 ,p); fprintf(o,".002 W .9 0 0 RGB S\n");
Conrec6(o,f,X,Y,M1,N1,-40 ,p); fprintf(o,".002 W .9 0 0 RGB S\n");
Conrec6(o,f,X,Y,M1,N1,-50 ,p); fprintf(o,".002 W .9 0 0 RGB S\n");
Conrec6(o,f,X,Y,M1,N1, 30 ,p); fprintf(o,".002 W 0 0 .9 RGB S\n");
Conrec6(o,f,X,Y,M1,N1, 40 ,p); fprintf(o,".002 W 0 0 .9 RGB S\n");
Conrec6(o,f,X,Y,M1,N1, 50 ,p); fprintf(o,".002 W 0 0 .9 RGB S\n");

fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
     system("epstopdf Z2sin1zMap.eps"); 
     system(    "open Z2sin1zMap.pdf"); //for mac
}

Latex generator of labels

% Warning: do not save the file below as "Z2sin1zMap.tex": at the compilation, the resulting *.pdf might overwrite the input Z2sin1zMap.pdf made with the code above. The Latex source below can be saved as Z2sin1zMapT.tex ; after the compilation, command «convert Z2sin1zMapT.pdf png8:Z2sin1zMapT.png» is supposed to produce the relatively compact file compatible with the wiki.

\documentclass[12pt]{article}
\usepackage{geometry}
\paperwidth 1940pt
\paperheight 1128pt
\textwidth 1140pt
\textheight 1180pt
\topmargin -103pt
\oddsidemargin -80pt
\usepackage{graphicx}
\usepackage{rotating}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \rme {\mathrm{e}}
\newcommand \sx {\scalebox}
\begin{document}
\begin{picture}(1920,1114)
\normalsize
%\put(40,0){\ing{oblakoV}}
\put(10,10){\includegraphics{Z2sin1zMap}}
\put(0,1090){\sx{3}{\(y\)}}
\put(-6,1012){\sx{3}{\(\frac{1}{2}\)}}
\put(-11,912){\sx{2.8}{\(\frac{4}{10}\)}}
\put(-11,812){\sx{2.8}{\(\frac{3}{10}\)}}
\put(-11,712){\sx{2.8}{\(\frac{2}{10}\)}}
\put(-11,612){\sx{2.8}{\(\frac{1}{10}\)}}
\put( -1,512){\sx{2.8}{\(0\)}}
\put(-11,412){\sx{2.8}{\(\frac{-\!1}{10}\)}}
\put(-12,312){\sx{2.8}{\(\frac{-\!1}{5}\)}}
\put(-13,212){\sx{2.8}{\(\frac{-\!3}{10}\)}}
\put(-13,112){\sx{2.8}{\(\frac{-\!2}{5}\)}}
\put(-13, 12){\sx{2.8}{\(\frac{-\!1}{2}\)}}
\put(88, -5){\sx{2.8}{\(-0.4\)}}
\put(188, -5){\sx{2.8}{\(-0.3\)}}
\put(288, -5){\sx{2.8}{\(-0.2\)}}
\put(388, -5){\sx{2.8}{\(-0.1\)}}
\put(515, -5){\sx{2.8}{\(0\)}}
\put(607, -5){\sx{2.8}{\(0.1\)}}
\put(707, -5){\sx{2.8}{\(0.2\)}}
\put(807, -5){\sx{2.8}{\(0.3\)}}
\put(907, -5){\sx{2.8}{\(0.4\)}}
\put(1007, -5){\sx{2.8}{\(0.5\)}}
\put(1107, -5){\sx{2.8}{\(0.6\)}}
\put(1207, -5){\sx{2.8}{\(0.7\)}}
\put(1307, -5){\sx{2.8}{\(0.8\)}}
\put(1407, -5){\sx{2.8}{\(0.9\)}}
\put(1507, -5){\sx{2.8}{\(1.0\)}}
\put(1607, -5){\sx{2.8}{\(1.1\)}}
\put(1707, -5){\sx{2.8}{\(1.2\)}}
\put(1807, -5){\sx{2.8}{\(1.3\)}}
%\put(1910, -1){\sx{2.3}{\(1.4\)}}
\put(1910, -2){\sx{3.1}{\(x\)}}
\put(484,540){\sx{3}{huge} }
\put(440,1031){\sx{3.3}{\rot{5}\(u\!=\!0\) \ero} }
\put(532,930){\sx{3.3}{\rot{90}\(u\!=\!0\) \ero} }
\put(484,891){\sx{3.2}{\rot{0}\(v\!=\!1\) \ero} }
\put(760,1040){\sx{2.9}{\rot{32}\(v\!=\!0.8\) \ero} }
\put(836,896){\sx{2.9}{\rot{24}\(v\!=\!0.6\) \ero} }
\put(878,780){\sx{2.9}{\rot{10}\(v\!=\!0.4\) \ero} }
\put(60,659){\sx{2.9}{\rot{0}\(v\!=\!0.2\) \ero} }
\put(886,659){\sx{2.9}{\rot{0}\(v\!=\!0.2\) \ero} }
\put(75,513){\sx{3}{\rot{0}\(v\!=\!0\) \ero} }
\put(900,513){\sx{3}{\rot{0}\(v\!=\!0\) \ero} }
\put(46,365){\sx{2.9}{\rot{0}\(v\!=\!-0.2\) \ero} }
\put(876,365){\sx{2.9}{\rot{0}\(v\!=\!-0.2\) \ero} }

\put(295,540){\sx{3}{\rot{80}\(v\!=\!0\) \ero} }
\put(50,464){\sx{2.8}{\rot{89}\(u\!=\!-0.2\) \ero} }
\put(766,484){\sx{3}{\rot{89}\(v\!=\!0\) \ero} }
\put(852,484){\sx{3}{\rot{89}\(u\!=\!0\) \ero} }
\put(1012,484){\sx{2.8}{\rot{89}\(u\!=\!0.2\) \ero} }
\put(194,426){\sx{3}{\rot{76}\(u\!=\!0\) \ero} }

\put(1164,484){\sx{2.8}{\rot{89}\(u\!=\!0.4\) \ero} }
\put(1326,482){\sx{2.9}{\rot{89}\(u\!=\!0.6\) \ero} }
\put(1498,484){\sx{2.9}{\rot{89}\(u\!=\!0.8\) \ero} }
\put(1676,484){\sx{3.1}{\rot{89}\(u\!=\!1\) \ero} }
\put(1858,482){\sx{2.8}{\rot{89}\(u\!=\!1.2\) \ero} }

\end{picture}
\end{document} 

References

Keywords

«ado.cin», «Asymptotic», «ChatGPT», «Complex map», «Conrec6.cin», «Restricted asymptotic», «Stricted asymptotic»,