File:SuTraMapLT.png

File
File history
File usage
Metadata

Size of this preview: 600 × 599 pixels. Other resolutions: 240 × 240 pixels | 2,010 × 2,008 pixels.

Original file ‎(2,010 × 2,008 pixels, file size: 153 KB, MIME type: image/png)

Summary

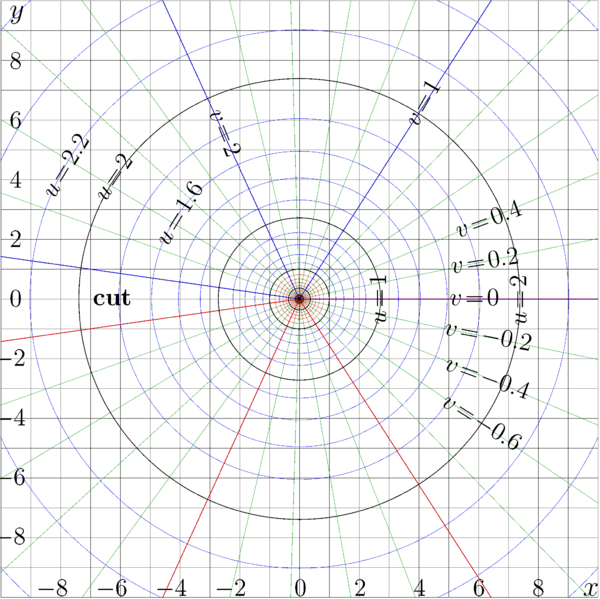
Complex map of Logarithm prepared for comparison to that for the example(s) of an Entire Function with Logarithmic Asymptotic.

The natural logarithm is shown assuming \(u+\mathrm i v= \log(x+\mathrm i y) \) in the \(x,y\) plane with lines \(u=\rm const\) and lines \(v=\rm const\) .

C++ generator of curves

/* files ado.cin and conto.cin sould be loaded in order to compile the code below. Other included files can be avoided, but better to load them too, in order to compile the generator of the similar map for the Entire Function with Logarithmic Asymptotic expressed through function SuTra ^[1]^[2]^[3].*/

/* Files ado.cin, conto.cin, Tania.cin, LambertW.cin, SuZex.cin should be loaded in order to compile the code below. */

 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
 using namespace std;
 #include<complex>
 typedef complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
 #include "conto.cin"

 #include "tania.cin"
 #include "LambertW.cin"
 #include "SuZex.cin"
 //#include "AuZex.cin" 

 z_type tra(z_type z) {return z+exp(z);}

// z_type sutra(z_type z){ if( Re(z)<2. || fabs(Im(z))>2. ) return log(suzex(z));
 z_type sutra(z_type z){ if( Re(z)<2. ) return log(suzex(z));
                                        return tra(sutra(z-1.));}

int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
 //DB x1=-1.1259817765745026; DO(n,8){ y=Re(suzex(x1)); x=y-1.; x1+=-1.2*x; printf("%18.16f %18.16f\n", x1,y);} getchar();
 int M=1001,M1=M+1;
 int N=1001,N1=N+1;
 DB X[M1],Y[N1];
 DB *g, *f, *w; // w is working array.
 g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
 f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
 w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
 char v[M1*N1]; // v is working array
 FILE *o;o=fopen("SuTraMapL.eps","w");  ado(o,2002,2002);
 fprintf(o,"1001 1001 translate\n 100 100 scale\n");
 fprintf(o,"1 setlinejoin 2 setlinecap\n");
 DO(m,M1) X[m]=-10+.02*(m-.5);
 DO(n,N1) Y[n]=-10+.02*(n-.5); 
 //for(n=0;n<N1;n++) { Y[n]=1.09*sinh((3./200.)*(n-200)); printf("%3d %9.6f\n",n,Y[n]); }
 for(m=-10;m<11;m++){M(m,-10) L(m,10)  }
 for(n=-10;n<11;n++){M(  -10,n) L(10,n)}
  fprintf(o,".006 W 0 0 0 RGB S\n");
 DO(m,M1)DO(n,N1){      g[m*N1+n]=999;
                        f[m*N1+n]=999;}
 DO(m,M1){x=X[m]; if(m/10*10==m) printf("x=%6.3f\n",x);
 DO(n,N1){y=Y[n]; z=z_type(x,y); //if(abs(z+2.)>.019)
//   c=-sutra(-z);
   c=log(z);
  p=Re(c); q=Im(c); if(p>-19 && p<19 && ( x<2. ||  fabs(q)>1.e-12 && fabs(p)>1.e-12) ){ g[m*N1+n]=p;f[m*N1+n]=q;}
        }}
 fprintf(o,"1 setlinejoin 1 setlinecap\n");
  p=1.2;q=.4;
 /*  p=9;q=.16;
  conto(o,g,w,v,X,Y,M,N,(15.3 ),-p,p); fprintf(o,".01 W .4 1 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(15.  ),-p,p); fprintf(o,".02 W 1 0 1 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(14.7 ),-p,p); fprintf(o,".01 W 1 .5 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(14.  ),-p,p); fprintf(o,".01 W .2 .2 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(13.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(12.  ),-p,p); fprintf(o,".03 W 0 0 1 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(11.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(10.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (9.  ),-p,p); fprintf(o,".03 W 0 1 1 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (8.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (7.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (6.  ),-p,p); fprintf(o,".04 W 0 .5 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (5.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (4.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (3.  ),-p,p); fprintf(o,".02 W 1 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (2.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (1.  ),-p,p); fprintf(o,".02 W .5 0 0 RGB S\n");
 */
 for(m=-8;m<8;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);fprintf(o,".007 W 0 .6 0 RGB S\n");
 for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);fprintf(o,".007 W .9 0 0 RGB S\n");
 for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);fprintf(o,".007 W 0 0 .9 RGB S\n");
 for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".02 W .8 0 0 RGB S\n");
 for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".02 W 0 0 .8 RGB S\n");
                conto(o,f,w,v,X,Y,M,N, (0.  ),-2*p,2*p); fprintf(o,".02 W .5 0 .5 RGB S\n");
 for(m=-16;m<17;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
 // fprintf(o,"0 setlinejoin 0 setlinecap\n");
 // M(-10,0)L(0,0) fprintf(o,"1 1 1 RGB .02 W S\n");
 //#include "plofu.cin"
 fprintf(o,"showpage\n");
 fprintf(o,"%c%cTrailer\n",'%','%');
 fclose(o);  free(f); free(g); free(w);
       system("epstopdf SuTraMapL.eps"); 
       system(    "open SuTraMapL.pdf"); //for macintosh
       getchar(); system("killall Preview"); // For macintosh
 return 0;
 }

Latex generator of labels

\documentclass[12pt]{article} % <br>
\paperwidth 2010px
\paperheight 2008px
\textwidth 2394px
\textheight 2300px
\topmargin -100px
\oddsidemargin -70px
\usepackage{graphics}
\usepackage{rotating}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\newcommand \rmi {\mathrm{i}}
\parindent 0pt
\pagestyle{empty}
\begin{document}
\parindent 0pt
\sx{1}{\begin{picture}(2002,2002) 
\put(30,1950){\sx{8}{$y$}}
\put(30,1780){\sx{7}{$8$}}
\put(30,1580){\sx{7}{$6$}}
\put(30,1380){\sx{7}{$4$}}
\put(30,1180){\sx{7}{$2$}}
\put(30,0980){\sx{7}{$0$}}
\put(-22,780){\sx{7}{$-2$}}
\put(-22,580){\sx{7}{$-4$}}
\put(-22,380){\sx{7}{$-6$}}
\put(-22,180){\sx{7}{$-8$}}
\put(120, 6){\sx{7}{$-8$}}
\put(320, 6){\sx{7}{$-6$}}
\put(520, 6){\sx{7}{$-4$}}
\put(720, 6){\sx{7}{$-2$}}
\put(988, 6){\sx{7}{$0$}}
\put(1188, 6){\sx{7}{$2$}}
\put(1388, 6){\sx{7}{$4$}}
\put(1588, 6){\sx{7}{$6$}}
\put(1788, 6){\sx{7}{$8$}}
\put(1958, 6){\sx{8}{$x$}}
\put(0,0){\ing{SuTraMapL}}
%\zoomax
\put(180,1340){\sx{7}{\rot{59}$u\!=\!2.2$\ero}}
\put(352,1330){\sx{7}{\rot{56}$u\!=\!2$\ero}}
\put(560,1180){\sx{7}{\rot{58}$u\!=\!1.6$\ero}}

\put(1540,1210){\sx{7}{\rot{20}$v\!=\!0.4$\ero}}
\put(1518,1090){\sx{7}{\rot{9}$v\!=\!0.2$\ero}}

\put(1400,1580){\sx{7}{\rot{60}$v\!=\!1$\ero}}
\put(700,1632){\sx{7}{\rot{-68}$v\!=\!2$\ero}}
\put(310,0984){\sx{7}{\bf cut}} \put(1510,0984){\sx{7}{$v\!=\!0$}}

\put(1296,0920){\sx{7}{\rot{90}$u\!=\!1$\ero}}
\put(1768,0916){\sx{7}{\rot{90}$u\!=\!2$\ero}}

\put(1490,886){\sx{7}{\rot{-11}$v\!=\!-0.2$\ero}}
\put(1490,768){\sx{7}{\rot{-20}$v\!=\!-0.4$\ero}}
\put(1480,648){\sx{7}{\rot{-32}$v\!=\!-0.6$\ero}}
\end{picture}}
\end{document}

Warning

Due to the permanent attacks by KGB (Roskomnadzor, «Фабрика троллей» ^[4]) on servers of cluster "Mizugadro", the codes (generators) of pictures run at different computers with different operational systems. Historically, some of them are not case-sensitive. This caused confusions with UPPERCASE/lowercase versions of the filenames.
Editor tries to eliminate the confusion, but some manual capitalization of some of the included files still may be required.
Editor hopes the problem with the attacks to be resolved after Demilitarization and denazification (Демилитаризация и денацификация) of Roskomnadzor (Роскомнадзор) and Lubyanka (Лубянка).
While KGB and Roskomnadzor attack Mizugadro, the response of the server may be slow. The copying of the content to other servers is encouraged - especially if you find some articles and/or pictures at mizugadro valuable, useful, important. In this way, «manuscripts don't burn.»^[5].

References

↑ https://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf
https://mizugadro.mydns.jp/PAPERS/2013hikari.pdf D.Kouznetsov. Entire Function with Logarithmic Asymptotic. Applied Mathematical Sciences, Vol. 7, 2013, no. 131, 6527 - 6541
↑ https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
https://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014 (in Russian)
↑ https://www.amazon.com/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862
https://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
↑ https://www.cambridge.org/core/services/aop-cambridge-core/content/view/D8A8A74976408CF7EC329827AFFFD3FC/S0003055421001507a.pdf/div-class-title-why-botter-how-pro-government-bots-fight-opposition-in-russia-div.pdf DENIS STUKAL, SERGEY SANOVICH, RICHARD BONNEAU, JOSHUA A. TUCKER. How Pro-Government Bots Fight Opposition in Russia. American Political Science Review (2022) 116, 3, 843–857.
↑ https://web.archive.org/web/20110606093139/http://lib.ru/BULGAKOW/master97_engl.txt Mikhail Bulgakov. The Master and Margarita (1997) © Translated from the russian by Richard Pevear and Larissa Volokhonsky. .. 'Forgive me, but I don't believe you,' Woland replied, 'that cannot be: manuscripts don't burn.' ..

Keywords

«ado.cin», «conto.cin», «Complex map», «Tania.cin», «LambertW.cin», «SuTra», «SuZex.cin», «Entire Function with Logarithmic Asymptotic», «Logarithm», «Superfunction», «Superfunctions»,

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	15:42, 9 January 2026		2,010 × 2,008 (153 KB)	T (talk \| contribs)	{{oq\|SuTraMapLT.png\|Original file ‎(2,010 × 2,008 pixels, file size: 153 KB, MIME type: image/png)\|480}} Complex map of Logarithm prepared for comparison to that for the example(s) of an Entire Function with Logarithmic Asymptotic. The natural logarithm is shown assuming \(u+\mathrm i v= \log(x+\mathrm i y) \) in the \(x,y\) plane with lines \(u=\rm const\) and lines \(v=\rm const\) . ==C++ generator of curves== /* files ado.cin and conto.cin sould be loaded in order...

You cannot overwrite this file.

File usage

The following page uses this file:

Entire Function with Logarithmic Asymptotic

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

File change date and time	04:33, 9 January 2026

[1] ttps://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf
https://mizugadro.mydns.jp/PAPERS/2013hikari.pdf D.Kouznetsov. Entire Function with Logarithmic Asymptotic. Applied Mathematical Sciences, Vol. 7, 2013, no. 131, 6527 - 6541

[2] ttps://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
https://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014 (in Russian)

[3] ttps://www.amazon.com/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862
https://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.

[4] ttps://www.cambridge.org/core/services/aop-cambridge-core/content/view/D8A8A74976408CF7EC329827AFFFD3FC/S0003055421001507a.pdf/div-class-title-why-botter-how-pro-government-bots-fight-opposition-in-russia-div.pdf DENIS STUKAL, SERGEY SANOVICH, RICHARD BONNEAU, JOSHUA A. TUCKER. How Pro-Government Bots Fight Opposition in Russia. American Political Science Review (2022) 116, 3, 843–857.

[5] ttps://web.archive.org/web/20110606093139/http://lib.ru/BULGAKOW/master97_engl.txt Mikhail Bulgakov. The Master and Margarita (1997) © Translated from the russian by Richard Pevear and Larissa Volokhonsky. .. 'Forgive me, but I don't believe you,' Woland replied, 'that cannot be: manuscripts don't burn.' ..

[1]

[2]

[3]

[4]

[5]