File:Sqrt2figL45eT.png

File
File history
File usage
Metadata

Size of this preview: 605 × 599 pixels. Other resolutions: 242 × 240 pixels | 2,180 × 2,159 pixels.

Original file ‎(2,180 × 2,159 pixels, file size: 1.07 MB, MIME type: image/png)

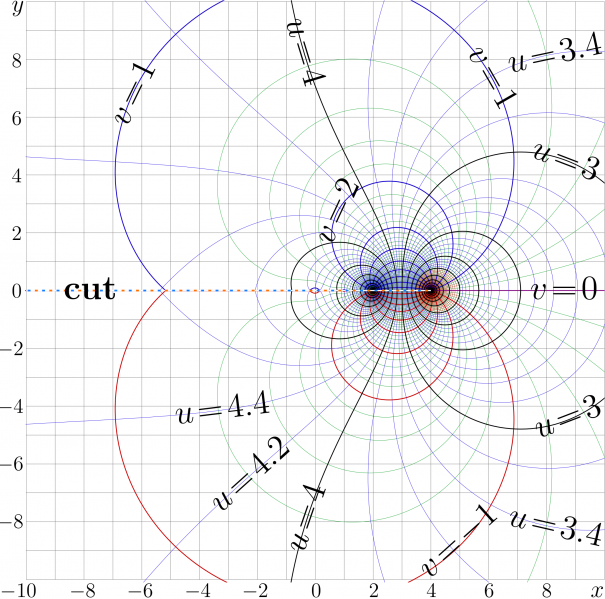
Complex map of the Abel function \(G\!=\!\mathrm{AuExp}_{\sqrt{2},5}\) of the exponential to base \(b\!=\!\sqrt{2}\) constructed at the fixed point \(L\!=\!4\) with Regular iteration and normalization \(G(5)\!=\!0\).

In the Mathematics of computation ^[1], this function is denoted as \(F_{4,5}^{-1}\).

The lines drawn correspond to \(u\!+\!\mathrm i v=G(x\!+\!\mathrm i y)\)

The map is used as Fig.9.7 at page 112 of book «Superfunctions», 2020 ^[2]^[3]
in order to confirm the successful construction and implementation of the growing Abelfunction \(\mathrm{AuExp}_{\sqrt{2},5}\) for the transfer function \(T\!=\!\exp_{\sqrt{2}}\) with the Regular iteration at the fixed point \(L\!=\!4\).

C++ generator of curves

Files ado.cin and conto.cin should be loaded to the working directory in order to compile the C++ code below.

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#include "conto.cin"

z_type f45E(z_type z){int n; z_type e,s; 
DB coeu[21]={1.,
0.44858743119526122890, .19037224679780675668, 
0.77829576536968278770e-1, 0.30935860305707997953e-1, 
0.12022125769065893274e-1, 0.45849888965617461424e-2,
0.17207423310577291102e-2, 0.63681090387985537364e-3,
0.23276960030302567773e-3, 0.84145511838119915857e-4,
0.30115646493706434120e-4, 0.10680745813035087964e-4,
0.37565713615564248453e-5, 0.13111367785052622794e-5,
0.45437916254218158081e-6, 0.15642984632975371803e-6,
0.53523276400816416929e-7, 0.18207786280204973113e-7,  
0.61604764947389226744e-8, 0.2e-8};
       e=exp(.32663425997828098238*(z-1.11520724513161));      
       s=coeu[20]; for(n=19;n>=0;n--) { s*=e; s+=coeu[n]; } 
//     s=coeu[19]; for(n=18;n>=0;n--) { s*=e; s+=coeu[n]; } 
       return 4.+s*e;}

z_type F45E(z_type z){ DB b=sqrt(2.);
                       if(Re(z)<-1.) return f45E(z);
                       return exp(F45E(z-1.)*log(b));
               }

z_type f45L(z_type z){ int n; z_type e,s;
DB Uco[21]={1,  
-.44858743119526122890,        .21208912005491969757, 
-.10218436750697167872,        0.49698683037371830337e-1, 
-0.2430759032611955221e-1,     0.11933088396510860210e-1,
-0.587369764200886206e-2,      0.289686728710575713e-2,
-0.1430908106079253664e-2,     0.7076637148565759223e-3,
-0.3503296158729878e-3,        0.17357560046634138e-3,
-0.86061011929162626e-4,       0.426959089012891e-4,
-0.2119302906819844809e-4,     0.1052442259960e-4,
-0.52285174354086e-5,          0.259844999161e-5,
-0.129178211214818578e-5,      0.4e-6  };
       z-=4.;
       s=Uco[19]; for(n=18; n>=0; n--){ s*=z; s+=Uco[n]; }
//     s=Uco[20]; for(n=19; n>=0; n--){ s*=z; s+=Uco[n]; }
//      return log(s*z)/.32663425997828098238 +1.1152091357215375; 
       return log(s*z)/.32663425997828098238 +1.11520724513161;
 }

z_type F45L(z_type z){ DB b=sqrt(2.);
                       if(abs(z-4.)>.4) return F45L(log(z)/log(b))+1. ;
                        return f45L(z);
               }
// #include"sqrt2f45E.cin"

main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
int M=501,M1=M+1;
int N=403,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("sqrt2figL45e.eps","w");  ado(o,202,202);
fprintf(o,"101 101 translate\n 10 10 scale\n");
DO(m,M1) X[m]=-10.+.04*(m-.5);
//DO(n,N1) Y[n]=-10.+.04*(n-.5);
 DO(n,200) Y[n]=sinh(3.*(n-200.5)/200.);
        Y[200]=-.0001;
        Y[201]= .0001;
for(n=202;n<N1;n++) Y[n]=sinh(3.*(n-200.5-2)/200.);
for(m=-10;m<11;m++) {M(m,-10)L(m,10)}
for(n=-10;n<11;n++) {M(  -10,n)L(10,n)} 
fprintf(o,"1 setlinejoin 2 setlinecap\n");
fprintf(o," .006 W 0 0 0 RGB S\n");
// z_type tm,tp,F[M1*N1];
DO(m,M1)DO(n,N1){      g[m*N1+n]=9999;
                       f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; 
DO(n,N1){y=Y[n]; z=z_type(x,y);        
//              c=F45E(z);
               c=F45L(z);
               p=Re(c); 
               q=Im(c);
               if(p>-15. && p<15. && q>-15. && q<15.
//              && fabs(p)>1.e-14
//              && fabs(q)>1.e-14
               ) { g[m*N1+n]=p; f[m*N1+n]=q;}
       }}
p=2.5; q=.8;
for(m=-10;m<10;m++)for(n=2              ;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (m+.1*n),-q,q);  fprintf(o,".01 W 0 .6 0 RGB S\n");
for(m=0;m<11;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);                  fprintf(o,".01 W .9 0 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);                    fprintf(o,".01 W 0 0 .9 RGB S\n");
for(m= 1;m<11;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".03 W .8 0 0 RGB S\n");
for(m= 1;m<11;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".03 W 0 0 .8 RGB S\n");
               conto(o,f,w,v,X,Y,M,N, (0.  ),-2*p,2*p); fprintf(o,".03 W .5 0 .5 RGB S\n");
for(m=-11;m<16;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".03 W 0 0 0 RGB S\n");
// #include "plofu.cin"
 M(-10,0)L(4,0)fprintf(o,"0 setlinecap .04 W 1 1 1 RGB S\n");
for(n=0;n<28;n++){ M(4-.5*(n+.2),0) L(4-.5*(n+.4),0) } fprintf(o,".06 W 1 .5 0 RGB S\n");
for(n=0;n<28;n++){ M(4-.5*(n+.7),0) L(4-.5*(n+.9),0) } fprintf(o,".06 W 0 .5 1 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
       system("epstopdf sqrt2figL45e.eps"); 
       system(    "open sqrt2figL45e.pdf"); //for macintosh
}

Latex generator of labels

%

 % Copyleft 2012 by Dmitrii Kouznetsov %<br>
 \documentclass[12pt]{article} %<br>
 \usepackage{geometry} %<br>
 \usepackage{graphicx} %<br>
 \usepackage{rotating} %<br>
 \paperwidth 1050pt %<br>
 \paperheight 1040pt %<br>
 \topmargin -98pt %<br>
 \oddsidemargin -99pt %<br>
 \textwidth 1100pt %<br>
 \textheight 1100pt %<br>
 \pagestyle {empty} %<br>
 \newcommand \sx {\scalebox} %<br>
 \newcommand \rot {\begin{rotate}} %<br>
 \newcommand \ero {\end{rotate}} %<br>
 \newcommand \ing {\includegraphics} %<br>
 \begin{document} %<br>
 \sx{5}{ \begin{picture}(208,205) %<br>
% \put(6,5){\ing{arctaniacontour}} %<br>
% \put(6,5){\ing{sqrt2figf45e}} %<br>
 \put(6,5){\ing{sqrt2figL45e}} %<br>
 \put(2,203.4){\sx{.7}{$y$}} %<br>
 \put(2,184){\sx{.6}{$8$}} %<br>
 \put(2,164){\sx{.6}{$6$}} %<br>
 \put(2,144){\sx{.6}{$4$}} %<br>
 \put(2,124){\sx{.6}{$2$}} %<br>
 \put(2,104){\sx{.6}{$0$}} %<br>
 \put(-3,84){\sx{.6}{$-2$}} %<br>
 \put(-3,64){\sx{.6}{$-4$}} %<br>
 \put(-3,44){\sx{.6}{$-6$}} %<br>
 \put(-3,24){\sx{.6}{$-8$}} %<br>
 \put(-2,00){\sx{.6}{$-10$}} %<br>
 \put( 22,0){\sx{.6}{$-8$}} %<br>
 \put( 42,0){\sx{.6}{$-6$}} %<br>
 \put( 62,0){\sx{.6}{$-4$}} %<br>
 \put( 82,0){\sx{.6}{$-2$}} %<br>
 \put(106,0){\sx{.6}{$0$}} %<br>
 \put(126,0){\sx{.6}{$2$}} %<br>
 \put(146,0){\sx{.6}{$4$}} %<br>
 \put(166,0){\sx{.6}{$6$}} %<br>
 \put(186,0){\sx{.6}{$8$}} %<br>
 \put(203,0){\sx{.7}{$x$}} %<br>
%<br>
 \put(020,103.5){\sx{.99}{\bf cut}} %<br>
 \put(182,103.5){\sx{.99}{$v\!=\!0$}} %<br>
%<br>  
\put(97,200){\rot{-73}\sx{.99}{$u\!=\!4$}\ero}%<br>
\put(175,182){\rot{12}\sx{.99}{$u\!=\!3.4$}\ero}%<br>
\put(182,153){\rot{-21}\sx{.99}{$u\!=\!3$}\ero}%<br>
\put(185,55){\rot{21}\sx{.99}{$u\!=\!3$}\ero}%<br>
\put(174,25){\rot{-13}\sx{.99}{$u\!=\!3.4$}\ero}%<br>
\put(103.4,15){\rot{71}\sx{.99}{$u\!=\!4$}\ero}%<br>
\put(074.6,29){\rot{42}\sx{.99}{$u\!=\!4.2$}\ero}%<br>
\put(059,60){\rot{7}\sx{.99}{$u\!=\!4.4$}\ero}%<br>
%<br>
\put(160,189){\rot{-60}\sx{.99}{$v\!=\!1$}\ero}%<br>
\put(147,6){\rot{42}\sx{.99}{$v\!=\!-1$}\ero}%<br>
%<br>
\put(42,163){\rot{64}\sx{.99}{$v\!=\!1$}\ero}%<br>
\put(113,122){\rot{65}\sx{.99}{$v\!=\!2$}\ero}%<br>
 \end{picture} %<br>
 } %<br>
 \end{document}

References

↑ http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf D.Kouznetsov, H.Trappmnn. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, v.271, July 2010, p.1727-1756.
↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - Lambert Academic Publishing, 2020/7/28
↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.

Keywords

«Abel function», «Abelexponential», «Abelfunction», «AuExp», «Base sqrt2», «BaseSqrt2», «Regular iteration», «SuExp», «Superfunction», «Superfunctions», «Table of superfunctions»,

«Суперфункции»,

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	17:50, 20 June 2013		2,180 × 2,159 (1.07 MB)	Maintenance script (talk \| contribs)	Importing image file

You cannot overwrite this file.

File usage

There are no pages that use this file.

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Horizontal resolution	59.06 dpc
Vertical resolution	59.06 dpc

[1] ttp://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf D.Kouznetsov, H.Trappmnn. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, v.271, July 2010, p.1727-1756.

[bookA-2] ttps://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - Lambert Academic Publishing, 2020/7/28

[bookM-3] ttps://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.

[1]

[2]

[3]