File:E1eplot8.png

From TORI
Jump to navigation Jump to search

Original file ‎(2,577 × 1,355 pixels, file size: 226 KB, MIME type: image/png)


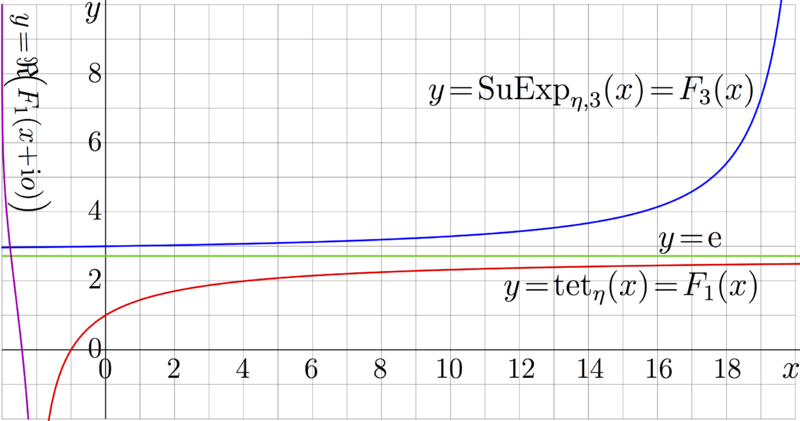
Explicit plot of the two superexponentials to base \(\ \eta=\exp(1/\mathrm e)\)

Description

Superexponential to base \(b\) is solution \(F\) of the transfer equation

\[ F(z+1)=\exp_b(F(z)) \]

For \(b\!=\!\eta\!=\!\exp(1/\mathrm e)\ \), the solutions that have specific asymptotic behavior are considered, they approach the fixed point \(\ \mathrm e \!\approx\! 2.71\ \) ; these solutions are described in Mathematics of Computation, 2012 [1] and in book about Superfunctions; both the Russian version «Суперфункции», 2014 [2] and the English version «Superfunctions», 2020.

Use of this image

Figure 1 of the article COMPUTATION OF THE TWO REGULAR SUPER-EXPONENTIALS TO BASE EXP(1/E), 2012 [1].

Figure 22.4 at page 138 of book «Суперфункции» about Superfunctions (Russian version, 2014) [2]

Figure 10.5 at page 127 pf book «Superfunctions» (English version, 2020) [3][4]

C++ generator of curves

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//using namespace std;
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "e1etf.cin"
#include "e1egf.cin"
#include "e1eti.cin"
void ado(FILE *O, int X, int Y)
{       fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%');
        fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y);
        fprintf(O,"/M {moveto} bind def\n");
        fprintf(O,"/L {lineto} bind def\n");
        fprintf(O,"/S {stroke} bind def\n");
        fprintf(O,"/s {show newpath} bind def\n");
        fprintf(O,"/C {closepath} bind def\n");
        fprintf(O,"/F {fill} bind def\n");
        fprintf(O,"/o {.1 0 360 arc C S} bind def\n");
        fprintf(O,"/times-Roman findfont 20 scalefont setfont\n");
        fprintf(O,"/W {setlinewidth} bind def\n");
        fprintf(O,"/RGB {setrgbcolor} bind def\n");}
//#include "ado.cin"
#define M(x,y) fprintf(o,"%6.3f %6.3f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.3f %6.3f L\n",0.+x,0.+y);
#define o(x,y) fprintf(o,"%6.3f %6.3f o\n",0.+x,0.+y);
int main(){ int j,k,m,n; DB p,q,t1,t3,u,v,w,x,y; z_type z,c,d;
//FILE *o;o=fopen("fige1e1.eps","w");ado(o,234,124);
FILE *o;o=fopen("e1eplot.eps","w");ado(o,234,124);
fprintf(o,"32 22 translate\n 10 10 scale\n");
for(m=-3;m<21;m++){if(m!=0){M(m,-2)L(m,10)}} 
for(n= -2;n<11;n++){if(n!=0){M(-3,n)L(20,n)}}   fprintf(o,".006 W 0 0 0 RGB S\n");
M(-3,0)L(20.2,0) M(0, -2)L(0,10.2)              fprintf(o,".03  W 0 0 0 RGB S\n");
M(-3,M_E)L(20.3,M_E)                            fprintf(o,".05  W 0 .8 0 RGB S\n");


fprintf(o,"1 setlinejoin 1 setlinecap\n");

DO(m,227){x=-3+.1*m; y=Re(E1EGF(x));    if(m==0)M(x,y)else L(x,y)} fprintf(o,".05 W 0 0 1 RGB S\n");

//DO(m,220){x=-1.5+.1*m; y=Re(E1ETF(x));        if(m==0)M(x,y)else L(x,y)} fprintf(o,".05 W 1 0 0 RGB S\n");
DO(m,221){x=-1.66+.1*m; y=Re(E1ETF(x)); if(m==0)M(x,y)else L(x,y)} fprintf(o,".05 W 1 0 0 RGB S\n");

DO(n,61){y=-2+.2*n; z=z_type(y,M_E*M_PI); x=Re(E1ETI(z)); 
                        printf("%9.4f %9.4f\n",x,y);
                        if(n==0)M(x,y)else L(x,y)} fprintf(o,".05 W .7 0 .7 RGB S\n");
fprintf(o,".03 W 0 0 0 RGB\n");
t1=-2.7982482;

/*
FILE *i;
i=fopen("walket1.txt","r");
DO(k,30){ j=fscanf(i,"%lf%lf%lf",&u,&v,&w);
         printf("%2d %5.2lf %14.10lf %14.10lf\n",j,u,v,w);
          if(j<3) break;
          if(v>10) break;
          o(v+t1,u)       
        }
printf("\n");

fclose(i);
i=fopen("walket2.txt","r");
DO(k,30){ j=fscanf(i,"%lf%lf%lf%lf",&y,&u,&v,&w);   if(j<4) break;
         printf("%5.2f %5.2lf %14.10lf %14.10lf\n",y,u,v,w);
                o(w+t1,y);
        }

printf("\n");
        t3=20.2874;
i=fopen("walket3.txt","r");
DO(k,30){ j=fscanf(i,"%lf%lf%lf",&u,&v,&w);
         printf("%2d %5.2lf %14.10lf %14.10lf\n",j,u,v,w);
          if(j<3) break;
          if(u>-10)       o(v+t3,u)       
        }
fclose(i);
*/

//fprintf(o,"0 setlinecap\n"); M(-2,0)L(-8,0) fprintf(o,".08 W 1 1 1 RGB S\n");
//DO(m,16){M(-2-.4*(m),0)L(-2-.4*(m+.5),0)} fprintf(o,".09 W 0 0 0 RGB S\n");
//M(-2,0)L(-10,0) fprintf(o,".04 W 0 0 0 RGB [.1 .1] 1 setdash  S\n");

fprintf(o,"showpage\n%cTrailer",'%'); fclose(o);
        system("epstopdf e1eplot.eps");
        system(    "open e1eplot.pdf"); //mac
//      system(    "xpdf e1eplot.pdf"); // linux

//q=1.e-14;
//for(n=-10;n<11;n++){z=q*n; y=Re(E1EGF(z)); 
//printf("E1EGF(%20.17f)=%20.17f\n",q*n,y);}

getchar(); system("killall Preview");// mac
}

Latex generator of labels

\documentclass[12pt]{article} 
%\paperwidth 472px 
%\paperheight 800px 
\paperwidth 232px 
\paperheight 122px 
\textwidth 704px 
\textheight 900px 
\topmargin -111px 
\oddsidemargin -73.4px 
\usepackage{graphics} 
\usepackage{rotating} 
\usepackage[usenames]{color}
\newcommand \sx {\scalebox} 
\newcommand \rot {\begin{rotate}} 
\newcommand \ero {\end{rotate}} 
\newcommand \ing {\includegraphics} 
\newcommand \rmi {\mathrm{i}} 
\parindent 0pt
\pagestyle{empty}
\begin{document} 
\begin{picture}(240,126)
%\put(0,0){\ing{fige1efre}}
%\put(0,0){\ing{fige1ew13}}
\put(0,0){\ing{e1eplot}}
\put( 26,119){\sx{.8}{$y$}}
\put( 27,100){\sx{.7}{$8$}}
\put( 27,80){\sx{.7}{$6$}}
\put( 27,60){\sx{.7}{$4$}}
\put( 27,40){\sx{.7}{$2$}}
\put( 27,20){\sx{.7}{$0$}}
\put( 30,14){\sx{.7}{$0$}}
\put( 50,14){\sx{.7}{$2$}}
\put( 70,14){\sx{.7}{$4$}}
\put( 90,14){\sx{.7}{$6$}}
\put(110,14){\sx{.7}{$8$}}
\put(128,14){\sx{.7}{$10$}}
\put(149,14){\sx{.7}{$12$}}
\put(169,14){\sx{.7}{$14$}}
\put(189,14){\sx{.7}{$16$}}
\put(209,14){\sx{.7}{$18$}}
\put(229,14){\sx{.8}{$x$}}
\put(6,120){\sx{.7}{\rot{-88}$y\!=\!\Re\!\Big(F_{1}(x\!+\!\rmi o)\Big)$\ero}}
%\put(183,95){\sx{1.}{$y\!=\!F_{3}(x)$}}
%\put(193,52){\sx{1.}{$y\!=\!\rme$}}
%\put(193,40){\sx{1.}{$y\!=\!F_{1}(x)$}}  %Dima's new latex does not like this
%\put(183,95){\sx{.8}{$y\!=\!F_{3}(x)$}}
%\put(136,38){\sx{.8}{$y\!=\!\mathrm{SuExp}_{\eta,3}(x)\!=\!F_{1}(x)$}}
%\put(148,95){\sx{.8}{$y\!=\!\mathrm{tet}_\eta(x)\!=\!F_{3}(x)$}}
\put(126,95){\sx{.8}{$y\!=\!\mathrm{SuExp}_{\eta,3}(x)\!=\!F_{3}(x)$}}
\put(148,38){\sx{.8}{$y\!=\!\mathrm{tet}_\eta(x)\!=\!F_{1}(x)$}}
\put(193,52){\sx{.8}{$y\!=\!\mathrm e$}}
\end{picture}
\end{document}

References

  1. ↑ 1.0 1.1 http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf
    http://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf
    H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation. Math. Comp., v.81 (2012), p. 2207-2227. ISSN 1088-6842(e) ISSN 0025-5718(p)
  2. ↑ 2.0 2.1 https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
    http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Pubilshing, 2014.
  3. ↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - 2020/7/28
  4. ↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current06:11, 1 December 2018Thumbnail for version as of 06:11, 1 December 20182,577 × 1,355 (226 KB)Maintenance script (talk | contribs)Importing image file

You cannot overwrite this file.

There are no pages that use this file.

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=File:E1eplot8.png&oldid=45377"