File:Duration5Li.jpg
Original file (1,419 × 295 pixels, file size: 73 KB, MIME type: image/jpeg)
Summary
Summary
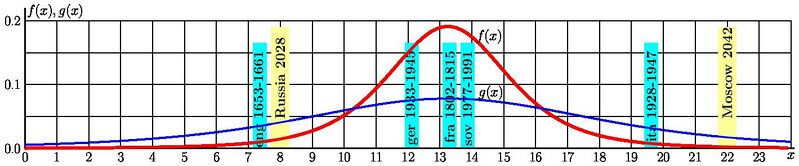
Picture prepared for Model First of articles Duration5 and Duration.
The picture is generated from the input file "i.txt" below with the C++ code below, together with two other pictures and table.
i.txt
1653 12 16 1661 04 23 eng
1802 08 04 1815 11 20 fra
1928 05 17 1947 12 27 ita
1933 03 24 1945 05 08 ger
1977 10 07 1991 08 20 sov
HtmlHeader.txt
<!DOCTYPE html><html>
<script type="text/x-mathjax-config">
MathJax.Hub.Config({
CommonHTML: { matchFontHeight: false },
tex2jax: {inlineMath: [['$','$'],['\\(','\\)']], processEscapes: true }
});
</script>
<script async src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.0/MathJax.js?config=TeX-AMS_CHTML"></script>
<head>
<meta charset="utf-8"/>
</head>
<body>
Main code
// routines ju24da.cin and Student.cin should be loaded for compilation of the code below.
// Files "i.txt" and "HtmlHeader.txt" above should be loaded for the execution
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include "ju24da.cin"
#include "Student.cin"
int main(){ int n,N=5; // The 6th case is not yet comleted. Here cases are numerated beginning with 0.
FILE *i,*o; // Input and Output pointers.
int Y1,M1,D1; //Year, Month, Day
int Y2,M2,D2; char str[N][4]; //just a string for each case
int Ya[N],Yb[N]; //the same as Y1,Y2, but arrays
int Days[N]; // Notaton "D" is confusive; better not to use it
double X[N]; // data for Linear scale (in years)
double L[N]; // data for Logaritmic scale
double x,y,p,q,r; // coordinates and other dummy variales
i=fopen("i.txt","r"); // input; computation of values of arrays X and L
for(n=0;n<N;n++){
fscanf(i,"%4d %2d %2d %4d %2d %2d %3s", &Y1,&M1,&D1, &Y2,&M2,&D2, str[n]); Ya[n]=Y1; Yb[n]=Y2;
Days[n]=daju24(Y2,M2,D2) - daju24(Y1,M1,D1) ; x=Days[n]/365.2422; X[n]=x; L[n]=log2(x);
printf("%4d %02d %02d %04d %02d %02d %3s %04d %6.4lf %6.4lf\n", Y1,M1,D1, Y2,M2,D2, str[n], Days[n], X[n], L[n]);
} fclose(i);
// Notations:
double t,T; // mean valies of data for the Linear scale and the Logarithmic scale;
double s,S; // estimates for standard error;
double c,C; // parameters of Student for mean value;
double v,V; // estimates for the standard error of the mean value (width of the distribution)
double c1,C1; // parameters of the Student Distribution for next measurement
double w,W; //estimates for the widths of distribution for the next measurement
// Linear scale
p=0.; for(n=0;n<N;n++) p+=X[n]; t=p/N; printf("tildeX=t=%5.2lf\n",t); // mean value
q=0.; for(n=0;n<N;n++) {r=X[n]-t; q+=r*r;}
s=sqrt(q/(N-1.)); printf("s=%5.2lf\n",s); // scale for standard error
c=sqrt(q/(N*(N-1.))); printf("c =%5.2lf\n",c ); // parameter for Student for mean value
c1=s*sqrt(1.+1./N); printf("c1=%5.2lf\n",c1); // parameter for Student for next value
v=sqrt(q/(N*(N-3.))); printf("z=%5.2lf\n",v); // spread for the mean value
w=s*sqrt((N-1.)/(N-3.))*sqrt(1.+1./N); printf("delta=%5.2lf\n",w); // spread for next value
o=fopen("Duration5Li.tex","w");
fprintf(o,"\\documentclass{standalone}\n");
fprintf(o,"\\usepackage{graphicx}\n");
fprintf(o,"\\usepackage{tikz}\n");
//fprintf(o,"\\newcommand \\sx {\\scalebox}\n"); // no need: \Huge does the job
fprintf(o,"\\begin{document}\n");
fprintf(o,"\\Huge\n");
fprintf(o,"\\begin{tikzpicture}[scale=2]\n");
fprintf(o,"\\draw [line width=0.981] (0,0) grid (24,4);\n");
fprintf(o,"\\draw [line width=2.3] (0,4.4) -- (0,0) -- (24.1,0) ;\n");
fprintf(o,"\\draw (-.08,4.3) node[right] {\\(f(x), g(x)\\)};\n");
fprintf(o,"\\definecolor{light}{rgb}{1,1,.6}\n"); // warning: no need ";" after to definecolor!!
fprintf(o,"\\definecolor{dark}{rgb}{0,1,1}\n");
fprintf(o,"\\draw[line width=32, light] (8,0.03) -- (8,3.8) ;\n");
fprintf(o,"\\draw (8,0.8) node[rotate=90,right] {\\bf Russia 2028};\n");
fprintf(o,"\\draw[line width=32, light] (22,0.03) -- (22,3.8) ;\n");
fprintf(o,"\\draw(22,0.8) node[rotate=90,right] {\\bf Moscow 2042};\n");
for(n=0;n<N;n++){
fprintf(o,"\\draw[line width=24, dark] (%5.3lf,0.03) -- (%5.3lf,3.3) ;\n",X[n], X[n]);
fprintf(o,"\\draw (%5.3lf,3.2) node[rotate=90,left] {\\bf %s %4d-%4d};\n",X[n],str[n],Ya[n],Yb[n]);
printf("%1d %s\n",n,str[n]);
}
for(n=0;n<5;n+=2) fprintf(o,"\\draw (0,%d) node[left] {%3.1f};\n",n,0.05*n);
for(n=0;n<24;n++) fprintf(o,"\\draw (%d,0) node[below] {%d};\n",n,n);
fprintf(o,"\\draw (%d,0) node[below] {\\(x\\)};\n",n);
printf("t=%9.6f ; c =%9.6f\n",t,c);
fprintf(o,"\\draw[line width=5, red] (0,0)");
for(n=1;n<241;n+=2)
{ x=.1*n; y=20*Student(N-1,(x-t)/c)/c; fprintf(o," -- (%6.3f,%6.3f)",x,y);
printf("curve 1: %6.4lf %6.4lf\n",x,y);
}
fprintf(o,";\n");
printf("t=%9.6f ; c1=%9.6f\n",t,c1);
for(n=0;n<241;n+=5)
{ x=.1*n; y=20*Student(N-1,(x-t)/c1)/c1;
if(n==0) fprintf(o,"\\draw[line width=3, blue] (0,%6.3f)",y);
else fprintf(o," -- (%6.3f,%6.3f)",x,y);
printf("curve 2: %6.4lf %6.4lf\n",x,y);
}
fprintf(o,";\n");
x=14.54; y=20*Student(N-1,(x-t)/c)/c;
fprintf(o,"\\draw (%5.2lf,%5.2lf) node[above] {\\(f(x)\\)};\n",x,y+.2);
//fprintf(o,";\n");
x=14.6; y=20*Student(N-1,(x-t)/c1)/c1;
fprintf(o,"\\draw (%5.2lf,%5.2lf) node[above] {\\(g(x)\\)};\n",x,y-.1);
//fprintf(o,";\n");
fprintf(o,"\\end{tikzpicture}\n");
fprintf(o,"\\end{document}\n");
fclose(o);
system("pdflatex Duration5Li.tex");
//system("open Duration5Li.pdf &");
// getchar();
// printf("The continuation is not yet ready\n");
// Logarithmic scale
p=0.; for(n=0;n<N;n++) p+=L[n]; T=p/N; printf("tildeL=T=%5.2lf\n",t); // mean value
q=0.; for(n=0;n<N;n++) {r=L[n]-T; q+=r*r;}
S=sqrt(q/(N-1.)); printf("S=%5.2lf\n",S); // scale for standard error
C=sqrt(q/(N*(N-1.))); printf("C =%5.2lf\n",C ); // parameter for Student for mean value
C1=S*sqrt(1.+1./N); printf("C1=%5.2lf\n",C1); // parameter for Student for next value
V=sqrt(q/(N*(N-3.))); printf("sigma=%5.2lf\n",V); // spread for the mean value
W=S*sqrt((N-1.)/(N-3.))*sqrt(1.+1./N); printf("Delta=%5.2lf\n",W); // spread for next value
o=fopen("Duration5Lo.tex","w");
fprintf(o,"\\documentclass{standalone}\n");
fprintf(o,"\\usepackage{graphicx}\n");
fprintf(o,"\\usepackage{tikz}\n");
//fprintf(o,"\\newcommand \\sx {\\scalebox}\n");
fprintf(o,"\\begin{document}\n");
fprintf(o,"\\Large\n");
//fprintf(o,"\\begin{tikzpicture}[scale=2]\n");
fprintf(o,"\\begin{tikzpicture}[scale=5]\n");
fprintf(o,"\\draw [line width=0.981] (0,0) grid (6,2);\n");
fprintf(o,"\\draw [line width=2.3] (0,2.2) -- (0,0) -- (6.1,0) ;\n");
fprintf(o,"\\definecolor{light}{rgb}{1,1,.6}\n");
fprintf(o,"\\definecolor{dark}{rgb}{0,1,1}\n");
fprintf(o,"\\draw[line width=12, light] (3,0.03) -- (3,1.4) ;\n");
fprintf(o,"\\draw (3,0.6) node[rotate=90,right] {\\bf Russia 2028};\n");
fprintf(o,"\\draw[line width=12, light] (%4.2f,0.03) -- (%4.2f,1.4) ;\n",log2(22.),log2(22.));
fprintf(o,"\\draw(%4.2f,0.6) node[rotate=90,right] {\\bf Moscow 2042};\n", log2(22.));
for(n=0;n<N;n++)
{
fprintf(o,"\\draw[line width=7, dark] (%5.3lf,0.04) -- (%5.3lf,0.4) ;\n",L[n], L[n]);
fprintf(o,"\\draw (%5.3lf,0.3) node[rotate=90,left] {\\bf %s};\n",L[n],str[n]);
printf("%1d %s\n",n,str[n]);
}
fprintf(o,"\\Huge\n");
fprintf(o,"\\draw (.04,2.1) node[right] {\\(F(L), G(L)\\)};\n");
for(n=0;n<3;n+=1) fprintf(o,"\\draw (0,%d) node[left] {%d};\n",n,n);
for(n=0;n<6;n++) fprintf(o,"\\draw (%d,0) node[below] {%d};\n",n,n);
fprintf(o,"\\draw (%d,0) node[below] {\\(L\\)};\n",n);
int m=1;
for(n=0;n<6;n++) {fprintf(o,"\\draw (%d,-0.2) node[below] {%d};\n",n,m); m*=2;}
fprintf(o,"\\draw (%d,-0.2) node[below] {\\(t\\), y.};\n",n);
printf("Lod scale, curve 1. T=%9.6f ; C=%9.6f\n",T,C);
fprintf(o,"\\draw[line width=5, red] (0,0)");
for(n=1;n<601;n+=2){x=.01*n; y=Student(N-1,(x-T)/C)/C; fprintf(o," -- (%6.4lf,%6.4lf)",x,y);}
fprintf(o,";\n");
printf("Lod scale, curve 2. T=%9.6f ; C1=%9.6f\n",T,C1);
for(n=0;n<601;n+=4)
{ x=.01*n; y=Student(N-1,(x-T)/C1)/C1;
if(n==0) fprintf(o,"\\draw[line width=3, blue] (0,%6.3f)",y);
else fprintf(o," -- (%6.3f,%6.3f)",x,y);
}
fprintf(o,";\n");
x=T; y=Student(N-1,(x-T)/C)/C;
fprintf(o,"\\draw (%5.2lf,%5.2lf) node[above] {\\(F(L)\\)};\n",x,y-.06);
//fprintf(o,";\n");
x=T; y=Student(N-1,(x-T)/C1)/C1;
fprintf(o,"\\draw (%5.2lf,%5.2lf) node[above] {\\(G(L)\\)};\n",x,y-.06);
//fprintf(o,";\n");
fprintf(o,"\\end{tikzpicture}\n");
fprintf(o,"\\end{document}\n");
fclose(o);
system("pdflatex Duration5Lo.tex");
//system("open Duration5Lo.pdf");
system("cp HtmlHead.txt Duration5tableBig.htm");
o=fopen("Duration5tableBig.htm","a");
fprintf(o,"<table border=1 cellpadding=6 cellspacing=3 style=\"border-collapse:collapse; text-align:center; border:1px solid\">\n");
// Do I need "solid:" above?
fprintf(o,"<tr><th>Quantity</th>\n");
//fprintf(o,"<th>Model First<br><small>(Normal distribution of durations)</small></th>\n");
//fprintf(o,"<th>Model Second<br><small>(Normal distribution of binary logarithms)</small></th></tr>\n");
fprintf(o,"<th><small>Normal distribution of durations)</small></th>\n");
fprintf(o,"<th><small>Normal distribution of the binary logarithms</small></th></tr>\n");
fprintf(o,"<tr><td>Distribution</td>\n");
fprintf(o,"<td>\\( X \\sim \\mathcal{N}(X_0, \\sigma_0^2) \\)</td>\n");
fprintf(o,"<td>\\( L = \\log_2 X \\sim \\mathcal{N}(L_0, \\ell_0^2) \\)</td></tr>\n");
fprintf(o,"<tr><td>mean; \\(N\\!=\\!\%d\\)</td>\n",N);
fprintf(o,"<td>\\(t=\\frac{1}{N} \\sum_{n=1}^N X_n\\approx%9.6f\\) [y.]</td>\n",t);
fprintf(o,"<td>\\(T=\\frac{1}{N} \\sum_{n=1}^N L_n\\approx%9.6f\\) <br>\n",T);
fprintf(o,"\\(\\exp_2(T)\\approx%9.6f\\) [y.]</td></tr>\n",pow(2.,T));
fprintf(o,"<tr><td>samle spread</td>\n");
fprintf(o,"<td>\\(s=\\sqrt{\\frac{1}{N-1} \\sum_{n=1}^N (X_n-t)^2}\\approx%9.6f\\) [y.]</td>\n",s);
fprintf(o,"<td>\\(S=\\sqrt{\\frac{1}{N-1} \\sum_{n=1}^N (L_n-T)^2}\\approx%9.6f\\)\n",S);
fprintf(o,"</td></tr>\n"); // only one line
fprintf(o,"<tr><td>scale for Student</td>\n");
fprintf(o,"<td>\\(c=\\sqrt{\\frac{1}{(N-1)N} \\sum_{n=1}^N (X_n\\!-\\!t)^2}\\approx%9.6f\\) [y.]</td>\n",c);
fprintf(o,"<td>\\(C=\\sqrt{\\frac{1}{(N-1)N} \\sum_{n=1}^N (L_n\\!-\\!T)^2}\\approx%9.6f\\)\n",C);
fprintf(o,"</td></tr>\n"); // only one line
fprintf(o,"<tr><td>Density for mean</td>\n");
fprintf(o,"<td>\\(f(x)=\\frac{1}{c} \\mathrm{Student}_{N-1}\\!\\left( \\frac{x-t}{c}\\right) \\ ~ \\) [y.\\(^{-1}\\)]</td>\n");
fprintf(o,"<td>\\(F(L)=\\frac{1}{C} \\mathrm{Student}_{N-1}\\!\\left( \\frac{L-T}{C}\\right)\\)");
fprintf(o,"</td></tr>\n"); // only one line
fprintf(o,"<tr><td>Spread for mean</td>\n");
fprintf(o,"<td>\\(v= \\sqrt{ \\int_{-\\infty}^{\\infty} f(x) ~ (x\\!-\\!t)^2 \\ \\mathrm d x \\ }\\)<br>\n");
fprintf(o," \\( = \\sqrt{\\frac{N-1}{N-3}}\\ c \\approx %9.6f\\ \\) [y.]</td>\n",v);
fprintf(o,"<td>\\(V= \\sqrt{ \\int_{-\\infty}^{\\infty} F(L) ~ (L\\!-\\!T)^2 \\ \\mathrm d L \\ }\\)<br>\n");
fprintf(o," \\( = \\sqrt{\\frac{N-1}{N-3}}\\ C \\approx %9.6f\\)</td>\n",V);
fprintf(o,"</tr>\n");
fprintf(o,"<tr><td>scale for Next</td>\n");
fprintf(o,"<td>\\(c_1 = s \\sqrt{1+1/N}\\approx%9.6f\\) [y.]</td>\n",c1);
fprintf(o,"<td>\\(C_1 = S \\sqrt{1+1/N}\\approx%9.6f\\)\n",C1);
fprintf(o,"</td></tr>\n"); // only one line
fprintf(o,"<tr><td>density for Next</td>\n");
fprintf(o,"<td>\\(g(x)=\\frac{1}{c_1} \\mathrm{Student}_{N-1}\\!\\left( \\frac{x-t}{c_1}\\right) \\ ~ \\) [y.\\(^{-1}\\)]</td>\n");
fprintf(o,"<td>\\(G(L)=\\frac{1}{C_1} \\mathrm{Student}_{N-1}\\!\\left( \\frac{L-T}{C_1}\\right)\\)");
fprintf(o,"</td></tr>\n"); // only one line
fprintf(o,"<tr><td>Spread for Next</td>\n");
fprintf(o,"<td>\\(w= \\sqrt{ \\int_{-\\infty}^{\\infty} g(x) ~ (x\\!-\\!t)^2 \\ \\mathrm d x \\ }\\)<br>\n");
fprintf(o," \\( = \\sqrt{\\frac{N-1}{N-3}}\\ c_1 \\approx %9.6f\\ \\) [y.]</td>\n",w);
fprintf(o,"<td>\\(W= \\sqrt{ \\int_{-\\infty}^{\\infty} G(L) ~ (L\\!-\\!T)^2 \\ \\mathrm d L \\ }\\)<br>\n");
fprintf(o," \\( = \\sqrt{\\frac{N-1}{N-3}}\\ C_1 \\approx %9.6f\\)</td>\n",W);
fprintf(o,"</tr>\n");
fprintf(o,"<tr><td>Naive for next</td>\n");
fprintf(o,"<td>\\(\\sqrt{s^2+c^2}\\approx %9.6f ~ \\) [y.]</td>\n",sqrt(s*s+c*c));
fprintf(o,"<td>\\(\\sqrt{S^2+C^2}\\approx %9.6f \\) </td>\n",sqrt(S*S+C*C));
fprintf(o,"</tr>\n");
fprintf(o,"<tr><td>sigma interval for mean</td>\n");
fprintf(o,"<td>\\(t\\pm v\\approx %9.6f, %9.6f ~ \\) [y.]</td>\n",t-v, t+v);
fprintf(o,"<td>\\(T\\pm V\\approx %9.6f, %9.6f ~ \\)<br>\n",T-V, T+V);
fprintf(o,"\\( \\exp_2( T\\pm V) \\approx %9.6f, %9.6f ~ \\) [y.]</td>\n",pow(2.,T-V), pow(2.,T+V));
fprintf(o,"</tr>\n");
fprintf(o,"<tr><td>sigma interval for next</td>\n");
fprintf(o,"<td>\\(t\\pm w\\approx %9.6f, %9.6f ~ \\) [y.]</td>\n",t-w, t+w);
fprintf(o,"<td>\\(T\\pm W\\approx %9.6f, %9.6f ~ \\)<br>\n",T-W, T+W);
fprintf(o,"\\( \\exp_2( T\\pm W) \\approx %9.6f, %9.6f ~ \\) [y.]</td>\n",pow(2.,T-W), pow(2.,T+W));
fprintf(o,"</tr>\n");
fprintf(o,"</table>\n");
fprintf(o,"</body></html>");
fclose(o);
//system("sleep 2; open Duration5tableBig.htm"); // need pause while showing the pdf?
o=fopen("Duration5compar2.tex","w");
fprintf(o,"\\documentclass{standalone}\n");
fprintf(o,"\\usepackage{graphicx}\n");
fprintf(o,"\\usepackage{tikz}\n");
fprintf(o,"\\newcommand \\sx {\\scalebox}\n"); // no need: \Huge does the job
fprintf(o,"\\begin{document}\n");
fprintf(o,"\\Huge\n");
fprintf(o,"\\begin{tikzpicture}[scale=2]\n");
fprintf(o,"\\draw [line width=0.981] (0,0) grid (30,8);\n");
fprintf(o,"\\draw [line width=2.3] (0,8.4) -- (0,0) -- (30.1,0) ;\n");
fprintf(o,"\\draw (0,8.3) node[right] {\\sx{1.8}{\\(g(x)\\) , blue ; \\(\\frac{G(\\log_2(x))}{x \\ \\log(2)}\\) , black}};\n");
fprintf(o,"\\definecolor{light}{rgb}{1,1,.6}\n"); // warning: no need ";" after to definecolor!!
fprintf(o,"\\definecolor{dark}{rgb}{0,1,1}\n");
fprintf(o,"\\draw[line width=32, light] (8,0.03) -- (8,3.8) ;\n");
fprintf(o,"\\draw (8,0.8) node[rotate=90,right] {\\bf Russia 2028};\n");
fprintf(o,"\\draw[line width=32, light] (22,0.03) -- (22,3.8) ;\n");
fprintf(o,"\\draw(22,0.8) node[rotate=90,right] {\\bf Moscow 2042};\n");
for(n=0;n<N;n++){
fprintf(o,"\\draw[line width=24, dark] (%5.3lf,0.03) -- (%5.3lf,3.3) ;\n",X[n], X[n]);
fprintf(o,"\\draw (%5.3lf,3.2) node[rotate=90,left] {\\bf %s %4d-%4d};\n",X[n],str[n],Ya[n],Yb[n]);
printf("%1d %s\n",n,str[n]);
}
for(n=0;n<9;n+=1) fprintf(o,"\\draw (0,%d) node[left] {\\sx{1.3}{%4.2f}};\n",n,0.01*n);
for(n=0;n<30;n++) fprintf(o,"\\draw (%d,0) node[below] {\\sx{1.3}{%d}};\n",n,n);
fprintf(o,"\\draw (%d,-.1) node[below] {\\sx{1.4}{\\(x\\)}};\n",n);
printf("t=%9.6f ; c1=%9.6f\n",t,c1);
for(n=0;n<303;n+=5)
{ x=.1*n; y=100*Student(N-1,(x-t)/c1)/c1;
if(n==0) fprintf(o,"\\draw[line width=3, blue] (0,%6.3f)",y);
else fprintf(o," -- (%6.3f,%6.3f)",x,y);
//printf("curve 2: %6.4lf %6.4lf\n",x,y);
}
fprintf(o,";\n");
printf("T=%9.6f ; T1=%9.6f\n",T,C1);
//fprintf(o,"\\draw[line width=3, black] (0,0)");
printf("T,C1=%20.16lf %20.16lf\n",T,C1);
for(n=1;n<304;n+=4)
{
x=.1*n; y=100./M_LN2*Student(N-1,(log2(x)-T)/C1)/C1/x;
if(n==1) fprintf(o,"\\draw[line width=3, black] (%6.3f,%6.3f)",x,y);
//if(n==1) fprintf(o,"\\draw[line width=3, blue] (%6.3f,%6.3f)",x,y);
else fprintf(o," -- (%6.3f,%6.3f)",x,y);
//printf("curve 2: %6.4lf %6.4lf\n",x,y);
}
fprintf(o,";\n");
fprintf(o,"\\end{tikzpicture}\n");
fprintf(o,"\\end{document}\n");
fclose(o);
system("pdflatex Duration5compar2.tex");
system("xpdf Duration5compar2.pdf");
}
Warning
The same code generates also two other pictures and the table for the same article.
References
Keywords
«Duration», «Duration5», «C++», «Duration5tableBig», «ju24da.cin», «Historic model», «Latex», «Likelihood density», «Normal distribution», «Nulling», «Probability density function», «Separation of powers», «Student Distribution», «Tikz», «Tikzpicture»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 20:15, 24 July 2025 | 1,419 × 295 (73 KB) | T (talk | contribs) | == Summary == {{oq|Duration5Li.jpg|}} ==Summary== Picture prepared for Model First of articles Duration5 and Duration. The picture is generated from the input file "i.txt" below with the C++ code below, together with two other pictures and table. ==i.txt== <poem> 1653 12 16 1661 04 23 eng 1802 08 04 1815 11 20 fra 1928 05 17 1947 12 27 ita 1933 03 24 1945 05 08 ger 1977 10 07 1991 08 20 sov </poem> ==HtmlHeader.txt== <pre> <!DOCTYPE html><html> <script type="text/x-mathjax-config"... |
You cannot overwrite this file.