File:Aufact.png

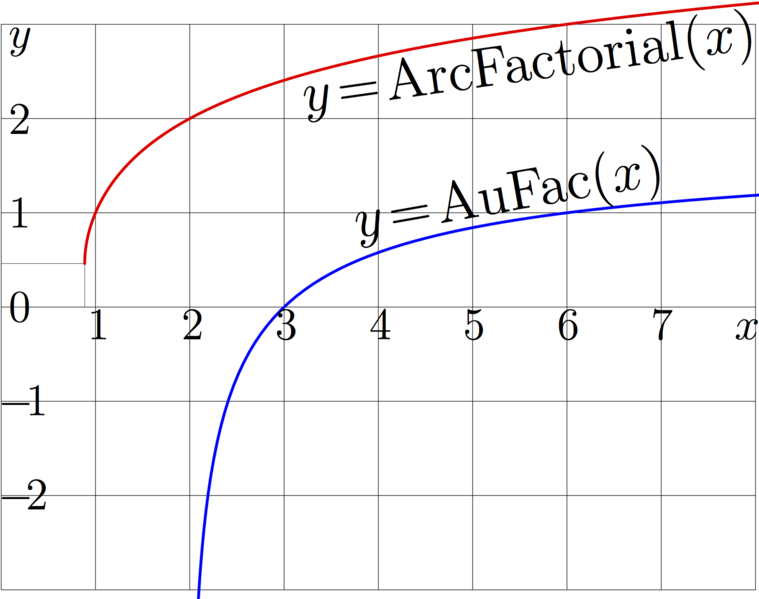
Explicit plot of function AuFac (blue), compared to ArcFactorial (red)

Function AuFac is Abelfunction of Factorial. It is described in the Moscow University Physics Bulletin, 2010 ^[1].

This plot is used as Fig.8.8 at page 99 of book «Superfunctions»^[2][3]
in order to avoid confusion of the two functions.

C++ generator of curves

// Files fac.cin, facp.cin, afacc.cin, ado.cin should be loaded in order to compile the code below

 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
// using namespace std;
 #include <complex>
 typedef std::complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
 #include "fac.cin"
 #include "facp.cin"
 #include "afacc.cin"
 #include "ado.cin"

 z_type arcsuperfac0(z_type z){ int n; z_type s, c, e;
 DB k=0.61278745233070836381366079016859252;
 DB U[19]={1.,                          -0.798731835172434541585621072345730147,
 0.69806411355936704552792746483306691, -0.6339640557572814865638000833478131,  
 0.5884152357911398848274232132172143,  -0.5538887519936519511632593654732843,  
 0.526547902598592454703287733600892,   -0.504191460428021561516069870422848,   
 0.48545298002933922263549078734881,    -0.46943468090947139273094056497701,
 0.4555204862393622788179080677150,     -0.4432726222110411295132308010077,     
 0.4323708863150174727399798603985,     -0.4225752531177612936293974175008,     
 0.413701949171132722406449918702,      -0.40560764595293667778491699902, 
 0.39817872478532299454624349817,       -0.391323,      0.384};
 //     z-=2.; s=U[15]*z; for(n=14;n>=0;n--){ s+=U[n]; s*=z;}
        z-=2.; s=U[18]*z; for(n=17;n>=0;n--){ s+=U[n]; s*=z;}
 return log(s)/k;}

 z_type arcsuperfac(z_type z){ if(abs(z-2.)<.12) return arcsuperfac0(z);
                                return  arcsuperfac(afacc(z))+1.;} // As in the Paper

 z_type abelfac(z_type z){ if(abs(z-2.)<.12) return arcsuperfac0(z)+0.91938596545217788;
                                return  abelfac(afacc(z))+1.;}
// #include "arcsuperfac.cin"

int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
 FILE *o;o=fopen("AbelFacPlo.eps","w");ado(o,810,640);
 #define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
 #define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
 fprintf(o,"1 315 translate\n 100 100 scale\n");
 fprintf(o,"2 setlinejoin 2 setlinecap\n");
 DO(m,9){M(m,-3)L(m,3)} for(n=-3;n<4;n++){M(0,n)L(8,n)}   fprintf(o,".006 W 0 0 0 RGB S\n");

 DB Bart=0.4616321449683622;
 DB Homer=0.8856031944108887;
 DB Liza1=1.5276760433847776;
 DB Liza2=0.3559463008501492;
 DB Liza3=-0.4620189870305121;

 M(0,Bart)L(Homer,Bart)L(Homer,0)  fprintf(o,".004 W 0 0 0 RGB S\n");
 fprintf(o,"1 setlinejoin 1 setlinecap\n");

 M(Homer,Bart)
 DO(m,86) { x=Homer+.001*(m*m+.5); y=Re(afacc(x)); L(x,y);}  fprintf(o,"1 0 0 RGB .03 W S\n");
 /* M(Homer,Bart)
 DO(m,38) { x=Homer+.001*(m*m+.5); y=Bart+
   Liza1*sqrt(x-Homer)+
   Liza2*(x-Homer);
   L(x,y);}
 fprintf(o,"0 0 0 RGB .006 W S\n"); // Expansion of ArcFactorial at the branch point 
 */
 DO(m,61){t=m/60.; x=2.09+6.*t*t; y=Re(abelfac(x)); if(m==0)M(x,y) else L(x,y);}
 fprintf(o,"0 0 1 RGB .03 W S\n"); 
 fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
        system("epstopdf AbelFacPlo.eps");      
        system(    "open AbelFacPlo.pdf");      //for LINUX
 //     getchar(); system("killall Preview");//for mac
 }
//

Latex generator of labels

\documentclass[12pt]{article}
\paperwidth 808pt
\paperheight 638pt
\textwidth 1800pt
\textheight 1800pt
\topmargin -72pt
\oddsidemargin -72pt 
\parindent 0pt
\pagestyle{empty}
\usepackage {graphics}
\usepackage{rotating}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\newcommand \sx {\scalebox}
\begin{document}
%\begin{picture}(806,580)
\begin{picture}(806,606)
%\put(0,0){\includegraphics{SuperFacPlot}} %
\put(0,0){\includegraphics{AbelFacPlo}}
\put(9,593){\sx{4}{$y$}}
\put(9,501){\sx{4}{$2$}}
\put(9,401){\sx{4}{$1$}}
\put(9,301){\sx{4}{$0$}}
\put(-2,201){\sx{4}{$-\!1$}}
\put(-2,101){\sx{4}{$-\!2$}}
\put(093,282){\sx{4}{$1$}}
\put(193,282){\sx{4}{$2$}}
\put(293,282){\sx{4}{$3$}}
\put(393,282){\sx{4}{$4$}}
\put(493,282){\sx{4}{$5$}}
\put(593,282){\sx{4}{$6$}}
\put(693,282){\sx{4}{$7$}}
\put(782,282){\sx{4}{$x$}}
%\put(352,540){\sx{4.2}{\rot{8.8}$y\!=\!\mathrm{ArcFactorial}(x)$\ero}}
\put(324,524){\sx{5}{\rot{8.8}$y\!=\!\mathrm{ArcFactorial}(x)$\ero}}
%\put(660,450){\sx{4}{\rot{83}$y\!=\!\mathrm{Factorial}(x)$\ero}} %
%\put(350,380){\sx{4.2}{\rot{10}$y\!=\!\mathrm{AuFac}(x)$\ero}}
\put(380,390){\sx{5}{\rot{10}$y\!=\!\mathrm{AuFac}(x)$\ero}}
\end{picture}
\end{document}

References

Keywords

«Abelfactorial», «Abelfunction», «AuFac», «Factorial», «Iterate», «Regular iteration», «SuFac», «Superfactorial», «Superfunction», «Superfunctions», «Square root of factorial»,

«Корень из факториала», «Суперфункции»,